09.3. Равносильность формул. Основные отношения равносильности

Определение 9.7. Формулы А, В алгебры предикатов сигнатуры σ Называются равносильными на алгебраической системе М(σ), если они принимают на М(σ) одинаковые значения при любом наборе значений предметных переменных, имеющих свободные вхождения переменных в А или В.

Из определения 9.7 видно, что равносильность тех или иных формул сигнатуры σ зависит от свойств алгебраической системы М(σ). Например, формулы "XA и $XA равносильны на любой одноэлементной системе, однако не равносильны в общем случае. Можно привести и менее тривиальные примеры. Изучение равносильностей, имеющих место для отдельных конкретных алгебраических систем, не отвечает целям и задачам математической логики как науки об общих закономерностях в рассуждениях. В связи с этим более ценным является следующее понятие равносильности.

Определение 9.8. Формулы алгебры предикатов сигнатуры σ называются Равносильными, если они равносильны на любой алгебраической системе сигнатуры σ. Равносильность формул А, В, как и равносильность высказываний будем обозначать в виде А º В.

Отметим следующие очевидные свойства равносильности формул.

Отношение равносильности формул является отношением эквивалентности на множестве всех формул сигнатуры σ, и, следовательно, все указанные формулы разбиваются на классы равносильных формул.

Если формула A¢ получена из А заменой некоторой подформулы В равносильной ей формулой В¢, то А¢ = А.

Приведем примеры равносильностей, называемых иногда основными равносильностями алгебры предикатов.

Перечисленные равносильности являются следствиями свойств логических операций, а потому имеют место для любых систем. В связи с этим их называют основными законами логики предикатов. Они постоянно (явно или неявно) используются при доказательствах утверждений во всех разделах математики.

Так, зачастую вместо теоремы вида А ® В доказывается равносильное утверждение`А ®`В. При этом используется закон контрапозиции 13 (табл.9.1). Закон исключенного третьего 15 обычно используется при доказательствах от противного, когда для доказательства теоремы А опровергают утверждение`А и отсюда на основании равносильности`A Ú A º и делают вывод об истинности А. Правило силлогизма 17 позволяет сводить доказательства теоремы вида А ® С к доказательству цепочек более простых утверждений, например, А ® В, В ® С.

Таблица 9.1

№	Равносильности	Название
1	AB º BA	Законы коммутативности
2	A Ú B º B Ú A
3	(AB)C º A(BC)	Законы ассоциативности
4	(A Ú B) Ú C º A Ú (B Ú C)
5	A(B Ú C) º AB Ú AC	Законы дистрибутивности
6	A Ú BC º (A Ú B)(A Ú C)
7	A(A Ú B) º A	Законы поглощения
8	A Ú AB º A
9	AA º A	Законы идемпотентности
10	A Ú A º A
11		Законы де Моргана
12
13		Закон контрапозиции
14		Закон двойного отрицания
15	И	Закон исключенного третьего
16	Л	Закон противоречия
17	(A ® B) & (B ® C) ® (A ® C) º И	Правило силлогизма
18	"Х"УА º "У"ХА	Правила перестановки одноименных кванторов
19	$Х$УА º $У$ХА
20		Правила отрицания кванторов
21
22	"X(A & B) º "XA & "XB	Законы дистрибутивности кванторов ", $ относительно операций & и v (соответственно)
23	$X(A Ú B) º $XA Ú $XB
24
25	ΔXA * B º δX(A * B), где δ — квантор " или $, * — операция & или v и формула В не содержит вхождений Х
26	δХА(Х) º δУА(У), где δ — квантор " или $, А(Х) — формула, не содержащая вхождений буквы У, а А(У) — формула, полученная из А(Х) заменой всех свободных вхождений Х на У

С другой стороны, в доказательствах иногда допускаются ошибки, состоящие в замене утверждения равносильным ему предложением. Так по аналогии с равносильностями 18-19 (см. табл.9.1), разрешающими переставлять одноименные кванторы, иногда переставляют и разноименные кванторы. Этого делать нельзя, поскольку и в общем случае формулы вида

"Х$УА и $У"ХА (9.3)

Не равносильны. Например, формула "Х$У(X < Y) истинна на N, а формула $Х"У(X < Y) ложна.

Аналогичные ошибки допускаются с использованием правила дистрибутивности кванторов $ и " относительно операций v и & соответственно. Можно показать, что формулы "Х(A Ú B) и "ХА Ú "XB, a также формулы $Х (A & B) и $ХА & $XB в общем случае не равносильны.

Заметим, что равносильность формул А, В эквивалентна истинности формулы (A ® B) & (B ® A) или двух формул A ® B, B ® A.

Однако практически зачастую бывает так, что из двух последних формул истинна только одна. Так, формулы (9.3) в общем случае не равносильны, но формула $У"ХА -> "Х$УА истинна на любой алгебраической системе.

Если формула А ® В истинна на системе М(σ), то при любом наборе значений предметных переменных, имеющих свободные вхождения в формулу А ® В, формула В принимает истинное значение всякий раз, когда истинным является значение А. В связи с этим говорят, что формула В является следствием формулы А.

Свойства отношения логического следования формулы из формул также широко используются при доказательствах. В рассуждениях при доказательствах иногда используется также известный в математической логике принцип двойственности.

Определение 9.9. Пусть А — формула алгебры предикатов, не содержащая операции «®». Формула, полученная из А заменой всех вхождений Ú на &, & на Ú, " на $, $ на ", называется Двойственной к А и обозначается через А*.

Очевидно, что (А*)* = А, и потому формулы А и А* называются двойственными. Двойственными называются и взаимозаменяемые операции Ú и &, а также кванторы " и $.

Теорема 9.10. Пусть А — формула алгебры предикатов, P1, …, PS суть все различные элементарные формулы в А, т. е.: A = A(P1, …, PS). Тогда имеет место равносильность формул:

.

Доказательство. Докажем теорему индукцией по рангу R формулы А. При R = 0 ее утверждение верно. Допустим, что оно верно для любой формулы ранга R < N и пусть R(A) = N + 1. Возможны пять случаев:

A = A1 & A2,

A = A1 Ú A2,

A = "XA1,

A = $XA1,

.

Рассмотрим случай A = A1 & A2. Тогда, используя предположение индукции, закон де Моргана (см. табл.9.1 п.11) и общие свойства равносильности, получим:

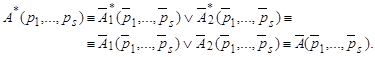
В трех следующих случаях рассуждения аналогичны. Вместо равносильности 11 в них используются соответственно равносильности 12, 20, 21 (см. табл.9.1). В последнем случае утверждение теоремы следует непосредственно из предположения индукции. Теорема доказана.

Следствие 9.11. (Принцип двойственности.)

Для любых формул А, В алгебры предикатов:

A º B Û A* º B*.

Принцип двойственности позволяет вместо двух равносильностей A º B и A* º B* доказывать лишь любую одну из них.

< Предыдущая		Следующая >