06.3. Метод Петрика нахождения тупиковых ДНФ
Рассмотрим табл.6.2, строки которой соответствуют простым импликантам функции F, а столбцы — конъюнкциям совершенной ДНФ (СДНФ). В каждую клетку записываем единицу, если соответствующая простая импликанта поглощает элементарную конъюнкцию и нуль — в противном случае. Такая таблица называется «импликантной таблицей».
Согласно определению, каждая Тупиковая ДНФ Определяется таким набором строк, что в таблице, образованной этими строками в каждом столбце имеется одна единица, причём из этого набора нельзя удалить ни одной строки так, чтобы при этом ни один столбец не стал нулевым.
Таблица 6.2
|
СДНФ Сокр. ДНФ |
1000 |
1100 |
1010 |
0101 |
0011 |
1110 |
1011 |
0111 | |
|
P1 |
1__0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
P2 |
101_ |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
P3 |
_001 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
P4 |
0_11 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
P5 |
01_1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Пусть в общем случае в таблице имеется N столбцов и M строк. Поставим в соответствие Простым импликантам сокращённой ДНФ переменные P1 … PM. Фиксируем некоторую дизъюнкцию простых импликант. Будем считать, что PI = 1, если I-я простая импликанта входит в эту дизъюнкцию и PI = 0, в противном случае. Запишем в виде формалы условие того, что рассматриваемая дизъюнкция является ДНФ функции. Для этого необходимо, чтобы в каждом столбце таблицы была хотя бы одна единица, т. е.
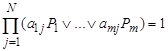 ,
,
Где ![]() — элемент матрицы (таблицы), стоящий в I-й строке и J-м столбце,
— элемент матрицы (таблицы), стоящий в I-й строке и J-м столбце, ![]() .
.
Эту формулу можно трактовать как КНФ некоторой двоичной функции от переменных P1 … PM, которая принимает значение 1 только на тех наборах переменных, которые соответствуют некоторым ДНФ исходной функции, и значение 0 — на наборах, которые соответствуют наборам импликант, не являющихся ДНФ исходной функции.
Заметим, что функция ![]() монотонна, так как формула 6.2.3 не содержит переменных с отрицаниями. Поэтому согласно утверждению 6.3 для нахождения её сокращённой ДНФ достаточно раскрыть скобки в формуле 6.2.3, а затем произвести все поглощения. Наконец, остаётся заметить, что в силу указанного выше свойства этой функции, её простые импликанты и только они будут давать тупиковые ДНФ исходной Функции F.
монотонна, так как формула 6.2.3 не содержит переменных с отрицаниями. Поэтому согласно утверждению 6.3 для нахождения её сокращённой ДНФ достаточно раскрыть скобки в формуле 6.2.3, а затем произвести все поглощения. Наконец, остаётся заметить, что в силу указанного выше свойства этой функции, её простые импликанты и только они будут давать тупиковые ДНФ исходной Функции F.
Для табл. 6.2 функция ![]() равна:
равна:
![]()
![]()
![]()
![]() .
.
Отсюда P1P3P5 даёт для F тупиковую форму:
![]() ,
,
А P1P2P4P5 даёт:
![]() .
.
| < Предыдущая | Следующая > |
|---|