02.1. Основные способы задания двоичных функций (продолжение). Нормальные формы двоичных функций
Всюду в этом параграфе рассматриваются формулы над классом ![]() . Обозначим через
. Обозначим через ![]() функцию
функцию
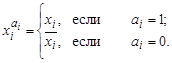
Очевидно, что ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() ,
, ![]() .
.
Определение 2.1. Элементарной конъюнкцией называется формула вида ![]() , где все переменные различны. Рангом элементарной конъюнкции называется число входящих в неё переменных.
, где все переменные различны. Рангом элементарной конъюнкции называется число входящих в неё переменных.
Непосредственно из определения 2.1 получаем, что элементарная конъюнкция ![]() принимает единичное значение в том и только том случае, когда
принимает единичное значение в том и только том случае, когда ![]() ,
, ![]() . Этот факт запомним как Свойство элементарных конъюнкций.
. Этот факт запомним как Свойство элементарных конъюнкций.
Определение 2.2. Дизъюнктивной нормальной формой (ДНФ) называется формула вида ![]() , где дизъюнкция берется по некоторым наборам
, где дизъюнкция берется по некоторым наборам ![]() , и
, и ![]() ,
, ![]() .
.
Обозначим через ![]() функцию, полученную из функции
функцию, полученную из функции ![]() фиксацией первых
фиксацией первых ![]() переменных значениями
переменных значениями ![]() . Из следующей теоремы вытекает, что любую двоичную функцию можно задать с помощью ДНФ.
. Из следующей теоремы вытекает, что любую двоичную функцию можно задать с помощью ДНФ.
Теорема 2.3 (о разложении функции). Пусть K такое, что ![]() . Тогда двоичную функцию
. Тогда двоичную функцию ![]() можно представить в виде:
можно представить в виде:
![]() . (2.1)
. (2.1)
Доказательство. Покажем, что функция, стоящая в левой и правой частях равенства (2.1), принимает одинаковое значение при одинаковых значениях переменной. Пусть ![]() . Тогда в силу свойств элементарных конъюнкций значение функции из правой части равно:
. Тогда в силу свойств элементарных конъюнкций значение функции из правой части равно:
![]() =
=
=![]() .
.
Теорема доказана.
Следствие 2.4.
![]() . (2.2)
. (2.2)
Доказательство. Следует из теоремы 2.3, если положить ![]()
Следствие 2.5.
![]() . (2.3)
. (2.3)
Доказательство. Вытекает из следствия 2.4 при перенумерации переменных.
Замечание 2.6. Разложение (2.2) называется разложением Шеннона, хотя формально ему не принадлежит.
Следствие 2.7.
![]() . (2.4)
. (2.4)
Доказательство. Следует из теоремы 2.3, если положить ![]() .
.
Замечание 2.8. В разложении (2.4) можно опустить все элементарные конъюнкции, которым соответствуют нулевые значения функций. Полученная в результате формула имеет вид:
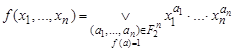 . (2.5)
. (2.5)
Определение 2.9. Равенство (2.5) называется Совершенной ДНФ (СДНФ) функции ![]() .
.
Как построить СДНФ функции ![]() ?
?
СДНФ двоичной функции легко построить по ее табличному заданию. С этой целью для каждого набора аргументов ![]() , на котором функция принимает единичное значение, строится элементарная конъюнкция ранга
, на котором функция принимает единичное значение, строится элементарная конъюнкция ранга ![]() по правилу:
по правилу:
![]() . (2.6)
. (2.6)
Затем берется дизъюнкция всех построенных элементарных конъюнкций. Приведём пример.
Пример 2.10. Пусть функция ![]() задана табл.2.1.
задана табл.2.1.
Таблица 2.1
|
Построим для неё СДНФ:
|
|
|
|
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
0 1 0 1 0 0 1 1 |
Поэтому:
![]()
![]()
![]()
![]()
![]()
Заметим, что СДНФ является частным случаем ДНФ. В ней все элементарные конъюнкции имеют ранг ![]() .
.
Отличительной особенностью СДНФ является то, что она однозначно определяется по функции ![]() с точностью до перестановки конституент.
с точностью до перестановки конституент.
Действительно, все элементарные конъюнкции в ней находятся во взаимно-однозначном соответствии с векторами ![]() из области истинности функции:
из области истинности функции: ![]() .
.
В отличие от СДНФ, ДНФ не однозначно соответствует функции. Так функция ![]() из предыдущего примера может быть записана в виде следующих ДНФ:
из предыдущего примера может быть записана в виде следующих ДНФ:
![]() .
.
Аналогично ДНФ вводятся конъюктивные нормальные формы (КНФ). Они являются конъюнкциями элементарных дизъюнкций ![]() и имеют вид
и имеют вид ![]() , где конъюнкция берется по некоторым наборам
, где конъюнкция берется по некоторым наборам ![]() ,
, ![]() ,
, ![]() . Как и в случае СДНФ можно показать, что функции
. Как и в случае СДНФ можно показать, что функции ![]() соответствует однозначно определенная КНФ (называемая Совершенная КНФ), в которой все элементарные дизъюнкции имеют ранг
соответствует однозначно определенная КНФ (называемая Совершенная КНФ), в которой все элементарные дизъюнкции имеют ранг ![]() . Её можно получить из СДНФ функции
. Её можно получить из СДНФ функции ![]() :
: 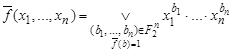 с помощью соотношений:
с помощью соотношений: ![]() ,
, ![]() . Из свойств 1.10 и 1.11 равносильных формул имеем:
. Из свойств 1.10 и 1.11 равносильных формул имеем:
![]()
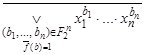 =
=
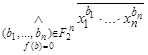 =
=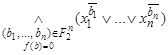 .
.
СКНФ функции ![]() легко строится по её табличному значению. Для функции
легко строится по её табличному значению. Для функции ![]() , заданной табл.2.1, получаем:
, заданной табл.2.1, получаем:
![]()
![]()
![]()
![]()
Поэтому
![]()
![]()
![]()
![]()
![]()
| < Предыдущая | Следующая > |
|---|