18.3. Основные NP-полные задачи. Сильная NP-полнота
В данном разделе устанавливается NP-полнота некоторых известных в различных приложениях задач. Предпочтение отдается графическим задачам как наиболее наглядным. Доказательство получается преобразованием в рассматриваемую задачу другой задачи, NP-полнота которой установлена. Для задач с целочисленными параметрами вводится важное понятие – сильная NP-полнота.
1. Пусть F(X1, …, XN) — формула от булевых переменных X1, …, XN в конъюнктивной нормальной форме, где каждая дизъюнкция имеет не более, чем три вхождения переменных. Задача проверки выполнимости таких формул называется Задачей 3-выполнимости (идентификатор: 3ВЫП).
Утверждение 18.6. Задача 3ВЫП является NP-полной.
Доказательство. Достаточно доказать, что ВЫПµ3ВЫП. Пусть F = D1D2 … DM — индивидуальная задача выполнимость от переменных X1, …, XN. Пусть DI = Z1 Ú Z2 Ú … Ú ZK и K > 3, ![]() . Положим
. Положим
![]()
![]()
Где Y1, …, YK-3 — новые переменные. Покажем, что:
DI выполнено тогда и только тогда, когда существует значение Y1, …, YK-3 такое, что ![]() выполнено;
выполнено;
DI не выполнено тогда и только тогда, когда для любых значений Y1, …, YK-3 ![]() не выполнено.
не выполнено.
Действительно:
DI = 0 Þ Z1 Ú Z2 Ú … Ú ZK = 0 Þ ![]()
![]() ;
;
DI = 1 Þ Z1 Ú Z2 Ú … Ú ZK = 1 Þ ![]() .
.
Укажем значения переменных Y1, …, YK-3, выполняющие ![]() (табл.18.3).
(табл.18.3).
Таблица 18.3
|
Y1 |
Y2 |
Y3 |
… |
YK-3 | |
|
Z1 = 1 |
0 |
0 |
0 |
… |
0 |
|
Z2 = 1 |
0 |
0 |
0 |
… |
0 |
|
Z3 = 1 |
1 |
0 |
0 |
… |
0 |
|
Z4 = 1 |
1 |
1 |
0 |
… |
0 |
|
… |
… |
… |
… |
… |
… |
|
ZK = 1 |
1 |
1 |
1 |
… |
1 |
Проделаем теперь процедуру замены каждой дизъюнкции DI на ![]() для каждого
для каждого ![]() с условием K > 3. Получим задачу 3-выполнимости за полиномиальное время. По доказанному имеем ВЫПµ3ВЫП, что и требовалось доказать.
с условием K > 3. Получим задачу 3-выполнимости за полиномиальное время. По доказанному имеем ВЫПµ3ВЫП, что и требовалось доказать.
Замечание. Можно доказать, что задача 2-выполнимости лежит в классе P.
2. Рассмотрим графическую задачу (идентификатор: КЛИКА): по произвольному графу G(V, E) и числу K узнать, имеется ли в графе G полный (граф называется полным, если любые две вершины соединены ребром) подграф с K вершинами (клика).
Утверждение 18.7. Задача КЛИКА является NP-полной.
Доказательство. Ясно, что КЛИКА Î NP, так как словом-отгадкой для задачи служит список вершин, составляющих клику и детерминированный алгоритм за полиномиальное время проверяет наличие ребра между каждой парой вершин. Покажем, что ВЫП µ КЛИКА.
Пусть F = D1D2…DM — произвольная индивидуальная задача ВЫП. Строим соответствующий граф GF следующим образом. Каждому вхождению переменной в F сопоставим вершину графа и присвоим ей обозначение (XA, I), где XA — вхождение переменного (a Î {0, 1}), I — номер соответствующей дизъюнкции. Вершины (XA, I) и (YB, J) соединим ребром в том и только в том случае, когда I ¹ J и XA не есть отрицание YB (т. е. X ¹ Y или, если X = Y, то a = b). Допустим, что F выполнима и пусть ![]() — соответствующий выполняющий набор. В каждом сомножителе F есть вхождение переменной, обратившее его в 1. Выберем по одному такому вхождению из каждой дизъюнкции. Рассмотрим соответствующее множество К вершин графа GF и покажем, что любые две такие вершины соединены ребром. Действительно, для вершин (XA, I) и (YB, J) нет соединяющего ребра лишь в случае I = J, либо
— соответствующий выполняющий набор. В каждом сомножителе F есть вхождение переменной, обратившее его в 1. Выберем по одному такому вхождению из каждой дизъюнкции. Рассмотрим соответствующее множество К вершин графа GF и покажем, что любые две такие вершины соединены ребром. Действительно, для вершин (XA, I) и (YB, J) нет соединяющего ребра лишь в случае I = J, либо ![]() . Но X ¹ Y, так как вхождения переменных взяты из разных дизъюнкций. Если
. Но X ¹ Y, так как вхождения переменных взяты из разных дизъюнкций. Если ![]() , то одно и то же значение переменного х не может одновременно обратить в 1 XA и YB. Значит, из выполнимости F следует наличие клики размера K в GF.
, то одно и то же значение переменного х не может одновременно обратить в 1 XA и YB. Значит, из выполнимости F следует наличие клики размера K в GF.
Обратно, пусть GF содержит клику размера K. Пусть это набор вершин ![]() . Покажем, что формула F выполнима. Положим
. Покажем, что формула F выполнима. Положим ![]() , и тогда
, и тогда ![]() . Значения остальных переменных положим произвольно. Противоречия в выборе значений переменных нет, так как если
. Значения остальных переменных положим произвольно. Противоречия в выборе значений переменных нет, так как если ![]() и
и ![]() соединены ребром, то a = b.
соединены ребром, то a = b.
По построению GF вершинам соответствуют вхождения переменных из разных дизъюнкций и так как число вершин равно K, то каждая дизъюнкция имеет вхождение переменного, обращающего в 1 при данных значениях переменных, значит и F обращается в 1. Построение GF проводится за полиномиальное время и, следовательно, ВЫП µ КЛИКА, что и требовалось доказать.
3. Говорят, что некоторое множество вершин ![]() графа G(V, E) образует вершинное покрытие графа, если для любого ребра E Î E найдется инцидентная ему вершина V Î V1 этого множества. Задача о вершинном покрытии (идентификатор: ВП) состоит в том, чтобы по произвольному графу G(V, E) и числу К узнать, имеет ли граф вершинное покрытие мощности K.
графа G(V, E) образует вершинное покрытие графа, если для любого ребра E Î E найдется инцидентная ему вершина V Î V1 этого множества. Задача о вершинном покрытии (идентификатор: ВП) состоит в том, чтобы по произвольному графу G(V, E) и числу К узнать, имеет ли граф вершинное покрытие мощности K.
Утверждение 18.8. Задача ВП является NP-полной.
Доказательство. Ясно, что ВПÎNP, так как словом-догадкой является список вершин соответствующего вершинного покрытия и правильность ответа проверяется за полиномиальное время. Покажем, что КЛИКА µ ВП.
Для графа G(V, E) строим граф G’, являющийся дополнением G до полного графа (т. е. G’ = (V, E’)), где E Î E’ Û E Ï E). Покажем, что А есть полный подграф в G Û дополнение А’ = V\A есть ВП в G’.
Действительно, пусть полный подграф с множеством вершин А лежит в G. Тогда, если бы для ребра ![]() графа G’ выполнялось бы
графа G’ выполнялось бы ![]() и
и ![]() , то должно быть, что ребра
, то должно быть, что ребра ![]() нет в G. Значит А’ = V\A — вершинное покрытие для G’.
нет в G. Значит А’ = V\A — вершинное покрытие для G’.
Обратно, если А’ образует вершинное покрытие графа G’, то всякое ребро, оба конца которого находятся в А, не может принадлежать G’ и содержится в G, т. е. в G имеется полный подграф с множеством вершин А.
Итак, задача о К-вершинном полном подграфе сводится к задаче о вершинном покрытии мощности K’ = N – K, N = |V|. Доказательство закончено.
Говорят, что множество вершин ![]() графа G(V, E) независимо, если никакие две вершины из V1 не связяны ребром. Задача о независимом множестве вершин (идентификатор: НВ) заключается в том, чтобы для произвольного графа G(V, E) и целого числа K выяснить, существует ли в G независимое множество из К вершин.
графа G(V, E) независимо, если никакие две вершины из V1 не связяны ребром. Задача о независимом множестве вершин (идентификатор: НВ) заключается в том, чтобы для произвольного графа G(V, E) и целого числа K выяснить, существует ли в G независимое множество из К вершин.
Утверждение 18.9. Задача НВ является NP-полной.
Доказательство аналогично предыдущему.
Приведем теперь без доказательства некоторые известные NP-полные проблемы. За доказательствами можно обратиться к книге: Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М., 1983.
5. Задача ГАМИЛЬТОНОВ ЦИКЛ (идентификатор: ГЦ).
Для произвольного графа G(V, E) требуется узнать, существует ли перестановка вершин ![]() такая, что выполнено:
такая, что выполнено: ![]()
6. Задача ЦЕЛОЧИСЛЕННЫЙ РЮКЗАК (идентификатор: ЦР).
Для произвольных натуральных чисел ![]() и K требуется узнать, существует ли набор целых чисел
и K требуется узнать, существует ли набор целых чисел ![]() , что выполнено
, что выполнено 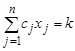 . Вариантом данной задачи является (0,1)-рюкзак, в которой требуется установить существование (0,1)-чисел
. Вариантом данной задачи является (0,1)-рюкзак, в которой требуется установить существование (0,1)-чисел ![]() с условием
с условием 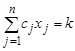 .
.
7. Множество ребер, разрезающих циклы. Для произвольного графа G(V, E) и целого числа к выяснить, существует ли множество ![]() , такое, что
, такое, что ![]() и каждый цикл графа G(V, E) содержит ребро из
и каждый цикл графа G(V, E) содержит ребро из ![]() .
.
8. Множество вершин, разрезающих циклы. То же, но только теперь ищется подмножество множества вершин.
9. Изоморфизм подграфу. Для заданных двух графов G(V1, E1) и H(V2, E2) выяснить, содержит ли граф G(V, E) подграф, изоморфный Н.
10. Проблема разрешимости диофантовых уравнений (в стандартном двоичном кодировании данных) вида
![]() .
.
В настоящее время известно большое число NP-полных задач из разных областей дискретной математики (несколько тысяч). Мы ограничимся приведением результата, полученного Шеффером Т. И. (1978), дающего бесконечную серию NP-полных проблем.
Пусть ![]() — любое конечное множество логических отношений. Логическое отношение определяется как некоторое подмножество из {0, 1}K для некоторого целого K ³ 1, при этом K называется рангом отношения. Определим S-формулу как произвольную конъюнкцию скобок, каждая вида
— любое конечное множество логических отношений. Логическое отношение определяется как некоторое подмножество из {0, 1}K для некоторого целого K ³ 1, при этом K называется рангом отношения. Определим S-формулу как произвольную конъюнкцию скобок, каждая вида ![]() , где
, где ![]() — переменные, число которых соответствует рангу
— переменные, число которых соответствует рангу ![]() . Проблема S-выполнимости — это проблема разрешения, является ли данная S-формула выполнимой.
. Проблема S-выполнимости — это проблема разрешения, является ли данная S-формула выполнимой.
Например, пусть R(X, Y, Z) — 3-местное логическое отношение с таблицей истинности {(1, 0, 0), (0, 1, 0), (0, 0, 1)}. Тогда формула R(X, Y, Z) × R(X, Y, U) × R(U, U, Y) выполнима и (X, Y, Z, U) = (0, 1, 0, 0) — ее выполняющий набор.
Результат Шеффера состоит в том, что проблема S-выполнимости полиномиально разрешима, если множество S удовлетворяет по крайней мере одному из приводимых ниже условий (в противном случае проблема NP-полна):
1) каждое отношение ![]() из S 0-выполнимо, т. е. (0, …, 0)
из S 0-выполнимо, т. е. (0, …, 0)![]() ;
;
2) каждое отношение ![]() из S 1-выполнимо, т. е. (1, …, 1)
из S 1-выполнимо, т. е. (1, …, 1)![]() ;
;
3) каждое отношение ![]() из S слабо положительно, т. е.
из S слабо положительно, т. е. ![]() логически эквивалентно формуле КНФ, имеющей самое большее одно переменное с отрицанием в каждой дизъюнкции;
логически эквивалентно формуле КНФ, имеющей самое большее одно переменное с отрицанием в каждой дизъюнкции;
4) каждое отношение ![]() из S слабо отрицательно, т. е.
из S слабо отрицательно, т. е. ![]() логически эквивалентно формуле КНФ, имеющей самое большее одно переменное без отрицания в каждой дизъюнкции;
логически эквивалентно формуле КНФ, имеющей самое большее одно переменное без отрицания в каждой дизъюнкции;
5) Каждое отношение ![]() из S мультиафинно, т. е.
из S мультиафинно, т. е. ![]() логически эквивалентно формуле, являющейся конъюнкцией линейных форм над полем GF(2);
логически эквивалентно формуле, являющейся конъюнкцией линейных форм над полем GF(2);
6) каждое отношение ![]() из S биюнктивно, т. е.
из S биюнктивно, т. е. ![]() логически эквивалентно формуле КНФ, имеющей самое большее вхождения двух переменных в каждой конъюнкции.
логически эквивалентно формуле КНФ, имеющей самое большее вхождения двух переменных в каждой конъюнкции.
Установим теперь NP-трудность некоторых задач, уже встречавшихся в курсе математической логики. Рассмотрим следующие задачи о булевых функциях.
Задача 1. РАВНОВЕРОЯТНОСТЬ БУЛЕВОЙ ФУНКЦИИ. Для данной булевой функции ![]() , заданной в КНФ, узнать, является ли она равновероятной (т. е. верно ли, что ее вес равен
, заданной в КНФ, узнать, является ли она равновероятной (т. е. верно ли, что ее вес равен ![]() ).
).
Задача 2. ЛИНЕЙНОСТЬ БУЛЕВОЙ ФУНКЦИИ. Для данной булевой функции ![]() , заданной в КНФ, узнать, является ли она линейной.
, заданной в КНФ, узнать, является ли она линейной.
Задача 3. СУЩЕСТВЕННОСТЬ ПЕРЕМЕННОГО. Для данных булевой функции ![]() в КНФ и целого числа К узнать, является ли переменное Xk существенным для F.
в КНФ и целого числа К узнать, является ли переменное Xk существенным для F.
Задача 4. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА. Для данной булевой функции ![]() в КНФ выяснить, образует ли F функционально полную систему (является ли F шефферовой).
в КНФ выяснить, образует ли F функционально полную систему (является ли F шефферовой).
Утверждение 18.10. Задачи (1 – 4) являются NP-трудными.
Доказательство.
Задача 1. Пусть ![]() — произвольная индивидуальная задача ВЫП, где
— произвольная индивидуальная задача ВЫП, где ![]() = D1…DM, DI — дизъюнкции. Определим функцию
= D1…DM, DI — дизъюнкции. Определим функцию ![]() = D1…DM Ú Y, где Y — новое переменное. Имеем
= D1…DM Ú Y, где Y — новое переменное. Имеем ![]() и, значит, КНФ для функции F* строится по функции F за полиномиальное время. Легко видеть, что
и, значит, КНФ для функции F* строится по функции F за полиномиальное время. Легко видеть, что ![]() . Значит, F* равновероятна тогда и только тогда, когда F не выполнима. Ясно, что условие «задача 1 Î P» влечет за собой ВЫП Î P, что означает задача 1 Î NPH.
. Значит, F* равновероятна тогда и только тогда, когда F не выполнима. Ясно, что условие «задача 1 Î P» влечет за собой ВЫП Î P, что означает задача 1 Î NPH.
Задача 2. Пусть ![]() — произвольная индивидуальная задача ВЫП. Определим функцию
— произвольная индивидуальная задача ВЫП. Определим функцию
![]() ,
,
Где Y1, Y2 — новые переменные. Ясно, что КНФ для функции F* строится по F за полиномиальное время. Легко видеть, что F* линейна тогда и только тогда, когда F не выполнима и условие «задача 2 Î P» влечет за собой ВЫП Î P, что означает задача 2 Î NPH.
Задача 3. Пусть ![]() — произвольная индивидуальная задача ВЫП. Образуем функцию
— произвольная индивидуальная задача ВЫП. Образуем функцию ![]() , где Y — новое переменное. Ясно, что Y существенно для F* тогда и только тогда, когда F — выполнима. Следовательно, «задача 3 Î P» влечет за собой ВЫП Î P, что означает задача 3 Î NP.
, где Y — новое переменное. Ясно, что Y существенно для F* тогда и только тогда, когда F — выполнима. Следовательно, «задача 3 Î P» влечет за собой ВЫП Î P, что означает задача 3 Î NP.
Задача 4. Пусть ![]() — произвольная индивидуальная задача ВЫП. Образуем функцию
— произвольная индивидуальная задача ВЫП. Образуем функцию
![]() .
.
Ясно, что КНФ для F* строится по F за полиномиальное время. Функция F* образует функционально полную систему тогда и только тогда, когда F выполнима. Действительно, если F не выполнима, то ![]() и F* не является функционально полной. Если F выполнима, то пусть
и F* не является функционально полной. Если F выполнима, то пусть ![]() - выполняющий набор. Тогда имеем
- выполняющий набор. Тогда имеем
![]() ,
,
![]() ,
,
Откуда следует не самодвойственность и не линейность функции F*. Очевидно, что F* не сохраняет нуль, не сохраняет единицу и не монотонна. Значит, функция F* удовлетворяет критерию Шеффера функциональной полноты. Следовательно, условие «задача 4 Î P» влечет за собой ВЫП Î P, что означает задача 4 Î NPН, что и требовалось доказать.
Замечание. Легко убедиться, что отрицание задачи 2, задачи 3 лежат в классе NP, и поэтому они NP-полны. Неизвестно, верно ли это для задач 1 и 4. Очевидно, что при табличном задании булевых функций рассмотренные задачи имеют полиномиальную сложность.
Разберем еще одно важное понятие, относящееся к обсуждаемому кругу вопросов. Рассмотрим задачу ЦЕЛОЧИСЛЕННЫЙ РЮКЗАК, которая, как отмечалось выше, является NP-полной. Пусть C1, …, CN, W — натуральные числа и спрашивается, существуют ли такие целые X1, …, XN ³ 0, что выполнено 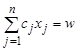 . Приведем один алгоритм решения данной задачи. Для индивидуальной задачи ЦР(C1, …, CN, W) построим ориентированный граф G(C1, …, CN, W) = (V, E), где V = {0, 1, …, W}, E = {(M, K), 0 £ M < K £ £ W и K – M = CJ для некоторого J £ N}. Значит, граф G имеет W + 1 вершину и O(Nw) дуг.
. Приведем один алгоритм решения данной задачи. Для индивидуальной задачи ЦР(C1, …, CN, W) построим ориентированный граф G(C1, …, CN, W) = (V, E), где V = {0, 1, …, W}, E = {(M, K), 0 £ M < K £ £ W и K – M = CJ для некоторого J £ N}. Значит, граф G имеет W + 1 вершину и O(Nw) дуг.
Утверждение 18.11. В графе G(C1, …, CN, W) имеется путь из 0 в W тогда и только тогда, когда индивидуальная задача ЦР(C1, …, CN, W) имеет решение.
Доказательство. Пусть (0 = I0, I1, …, IM = W) — нужный путь в графе G. Рассмотрим набор чисел (S1, …, SM) = (I1 – I0, …, IM – IM-1). Все эти числа содержатся среди чисел {C1, …, CN} согласно определению графа G. Кроме того, имеем 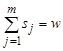 . Отсюда следует, что уравнение
. Отсюда следует, что уравнение 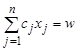 разрешимо в неотрицательных целых числах, причем XJ равно числу появлений CJ в последовательности (S1, …, SM).
разрешимо в неотрицательных целых числах, причем XJ равно числу появлений CJ в последовательности (S1, …, SM).
Обратно, если 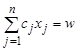 для неотрицательных целых чисел X1, …, XN, то можно восстановить некоторый путь из 0 в W в графе G, если положить (S1, …, SM) = (
для неотрицательных целых чисел X1, …, XN, то можно восстановить некоторый путь из 0 в W в графе G, если положить (S1, …, SM) = (![]() ) и путь из 0 в W имеет вид (0 = I0, I1, …, IM = W), где I1 = S1, I2 = S1 + S2, …, IM = S1 + … + SM. Доказательство завершено.
) и путь из 0 в W имеет вид (0 = I0, I1, …, IM = W), где I1 = S1, I2 = S1 + S2, …, IM = S1 + … + SM. Доказательство завершено.
Утверждение 18.12. Любая индивидуальная задача ЦР может быть решена за О(Nw) действий.
Доказательство. По данным C1, …, CN, W строим граф G за О(Nw) действий. Затем за О(Nw) действий проверяем существует ли путь из 0 в W, используя способ пометок: вершину 0 помечаем 0, вершины, достижимые из 0 за 1 шаг, помечаем 1 и т. д. Если W получает пометку, то задача разрешима, если нет, то неразрешима. Доказательство завершено.
Приведенный результат показывает, что NP-полная задача ЦЕЛОЧИСЛЕННЫЙ РЮКЗАК решается с помощью алгоритма с временной сложностью О(Nw) — полиномиального и, следовательно, доказано, что P = NP и можно считать ненужным предыдущее и последующее обсуждение теории NP-полноты. Дело в том, что оценка О(Nw) не является полиномиальной функцией от длины входа, так как целые числа в экономном кодировании должны задаваться в двоичной системе счисления. В то же время приведенный результат важен, так как он показывает, что NP-полные задачи имеют разную «сложность».
Для задач с числовыми параметрами введем следующие определения. Пусть I — индивидуальная вычислительная задача, т. е. с числовыми параметрами. Обозначим через Num(I) — наибольшее целое число, появляющееся в I.
Определение 18.13. Пусть А — вычислительная задача и F:N à N — числовая функция. Обозначим через AF подзадачу задачи А, в которой берутся индивидуальные задачи I, для которых выполнено Num(I) £ F(|I|). Говорят, что задача А Сильно NP-Полна, если для некоторого полинома P(N) задача AP является NP-полной.
Замечание. Можно показать, что задачи КЛИКА, ГАМИЛЬТОНОВ ЦИКЛ являются сильно NP-полными, а задачи (0,1)-РЮКЗАК и ЦЕЛОЧИСЛЕННЫЙ РЮКЗАК не являются таковыми.
Определение 18.14. Алгоритм АЛГ для задачи А называют Псевдополиномиальным, если он решает любую индивидуальную задачу I Î A за время, ограниченное полиномом (двух переменных) от |I| и Num(I). Значит, алгоритм со сложностью О(Nw) для задачи ЦЕЛОЧИСЛЕННЫЙ РЮКЗАК является псевдополиномиальным (ясно, что для индивидуальной задачи I ЦР Num(I) = W).
Отметим, что сильная NP-полнота задачи делает маловероятным существование псевдополиномиального алгоритма точно также, как NP-полнота задачи делает маловероятным существование полиномиального алгоритма.
Утверждение 18.15. Если P ¹ NP, то ни для одной сильно NP-полной задачи не существует псевдополиномиального алгоритма.
Доказательство. Пусть А — сильно NP-полная задача. Значит, для некоторого полинома P(N) задача АP является NP-полной. Далее, пусть для А существует псевдополиномиальный алгоритм АЛГ, который решает любую индивидуальную задачу I Î A за время Q(|I|, Num(I)) для некоторого полинома Q от двух переменных. Тогда очевидно, что алгоритм АЛГ решает NP-полную задачу АP за время Q(N, P(N)) — что является полиномиальной оценкой. Получено противоречие при P ¹ NP, что и требовалось доказать.
| < Предыдущая | Следующая > |
|---|