16.1. Алгоритмически неразрешимые проблемы

В данном разделе устанавливается алгоритмическая неразрешимость ряда проблем, относящихся к теории алгоритмов.

Будем рассматривать так называемые Массовые проблемы. Массовая проблема представляет собой бесконечную серию индивидуальных задач. Например, индивидуальной задачей является такая: обладает ли заданным свойством Q конкретная частично рекурсивная функция. Совокупность всех таких задач (для всех частично рекурсивных функций) образует массовую проблему распознавания свойства Q. Мы ограничимся такими массовыми проблемами, в которых все индивидуальные задачи имеют двузначный ответ («ДА» или «НЕТ»).

Массовая проблема П является Алгоритмически разрешимой, если соответствующая характеристическая функция F, которая определяется соотношением:

Является вычислимой.

Решая конкретную массовую проблему, следует считаться с возможностью, что она может оказаться алгоритмически неразрешимой, поэтому необходимо иметь представление о технике доказательства неразрешимости. Основной метод, применяемый в доказательствах алгоритмической неразрешимости, базируется на следующем рассуждении. Пусть имеем две массовые проблемы П1 и П2. Пусть имеется алгоритм А, который по всякой индивидуальной задаче строит индивидуальную задачу такую, что выполнено: имеет ответ «ДА» тогда и только тогда, когда имеет ответ «ДА». В этом случае говорят, что проблема П1 сводится к проблеме П2. Если проблема П1 неразрешима, то проблема П2 также неразрешима. Действительно, пусть это не так, и проблема П2 разрешима. Тогда можно построить разрешающий алгоритм для проблемы П1. Берем произвольную индивидуальную задачу . Имея алгоритм А, строим индивидуальную задачу . Теперь применяем к задаче существующий по предположению разрешающий алгоритм для проблемы П2. Если задача имеет ответ «ДА», то для задачи полагаем ответ «НЕТ». Поскольку, по условию, проблема П1 неразрешима, то получим противоречие. Значит, проблема П2 неразрешима. Данное рассуждение называется Методом сводимости, и его применение возможно, если уже имеется запас проблем, алгоритмическая неразрешимость которых уже установлена. Приведем теперь некоторые из таких проблем.

Рассмотрим так называемую Проблему самоприменимости Машин Тьюринга. Она заключается в следующем. Рассматриваются машины Тьюринга, внешние алфавиты которых содержат символы 0,1 (наряду с другими). Для каждой машины Тьюринга Т построим Код(Т), который является (0,1)-словом, и запустим машину Т в начальной конфигурации Q1Код(Т). Если машина Т останавливается (т. е. попадает в заключительное состояние) через конечное число шагов, то она называется Самоприменимой, в противном случае — Несамоприменимой. Заметим, что имеются как самоприменимые, так и несамоприменимые машины Тьюринга. Например, несамоприменимой будет машина Т1, у которой все команды имеют вид QIAJ à QIAJE (в правых частях команд нет заключительного состояния), самоприменимой будет машина Т1, у которой все команды имеют вид QIAJ à Q0AJE (в правых частях всех команд имеется заключительное состояние). Проблема самоприменимости состоит в том, чтобы по любой машине Тьюринга Т определить, является ли она самоприменимой или нет. Условимся, что машина Тьюринга М решает проблему самоприменимости, если для любой машины Т начальную конфигурацию Q1Код(Т) она переводит в Q01, если машина Т самоприменима, и в Q00, если машина Т несамоприменима.

Теорема 16.1. Не существует машины Тьюринга М, решающей проблему самоприменимости, т. е. проблема самоприменимости алгоритмически неразрешима.

Доказательство. Предположим противное, т. е. пусть существует машина Тьюринга М, решающая проблему самоприместимости в указанном выше смысле. Построим новую машину М0, добавив новое состояние и объявив его заключительным, а также добавив новые команды для состояния Q0, которое было заключительным в М:

Q01 à Q01E; (a)

Q00 à 0E. (b)

Рассмотрим теперь работу машины М0. Пусть Т — произвольная машина. Если Т — самоприменима, то начальная конфигурация Q1Код(Т) перейдет с помощью команд машины МO через конечное число шагов в конфигурацию Q01, далее применяется команда (a), и машина М0 никогда не остановится. Если Т — несамоприменима, то начальная конфигурация Q1Код(Т) перейдет с помощью команд машины М через конечное число шагов в конфигурацию Q00, далее применяется команда (b), и машина М0 остановится. Значит, машина М0 применима к кодам самоприменимых машин Т и не применима к кодам самоприменимых машин Т. Теперь рассмотрим Код(М0) и применим машину М0 к начальной конфигурации Q1Код(М0). Сама машина М0 является либо самоприменимой, либо несамоприменимой. Если М0 самоприменима, то по доказанному, она никогда не остановится, начав с Q1Код(М0), и потому она несамоприменима. Если М0 несамоприменима, то по доказанному, она останавливается через конечное число шагов, начав с Q1Код(М0), и потому она самоприменима. Получили противоречие, которое является следствием допущения существования машины М0, решающей проблему самоприменимости, что и требовалось доказать.

Приведем еще один пример неразрешимой проблемы.

Проблемой останова Называют проблему, заключающуюся в том, чтобы по любой машине Тьюринга Т и слову Р в ее внешнем алфавите узнать, применима ли Т к начальной конфигурации Q1Р.

Проблема останова алгоритмически неразрешима, так как если бы она была разрешимой, то, взяв в качестве Р слово Код(Т), мы получили бы разрешимость проблемы самоприменимости.

Приведем теперь неразрешимые проблемы, связанные с проверкой свойств частично рекурсивных функций. Пусть U(N, X) — универсальная функция для одноместных частично рекурсивных функций и соответствующая ей нумерация функций

F0(X), F1(X), …, FN(X), …, (16.1)

Где FN(X) = U(N, X).

Теорема 16.2. Проблема «функция FN всюду определена», N ΠN0 алгоритмически неразрешима.

Доказательство. Определим характеристическую функцию данной проблемы

.

Определим новую функцию Ф(X), где

.

Заметим, что функция Ф(X) всюду определена. Кроме того,

.

Нам нужно доказать невычислимость функции G. Ясно, что из вычислимости функции G следует вычислимость функции Ф. Предположим, что функция Ф вычислима. Тогда существует число N такое, что Ф(X) = U(N, X) = FN(X). Поскольку Ф(X) — всюду определена, то должно быть G(N) = 1. Значит, имеем Ф(N) = FN(N) и Ф(N) = FN(N) + 1. Поскольку при X = N функция Ф(X) определена, то получаем противоречие. Следовательно, Ф(X) — невычислима, откуда следует, что функция G(X) — невычислима, что и требовалось доказать.

Обозначим через WN область определения функции FN(X) в последовательности (16.1).

Теорема 16.3. Проблема «N ΠWN», N ΠN0 алгоритмически неразрешима.

Доказательство. Рассмотрим характеристическую функцию проблемы:

И построим новую функцию G(X), где

Ясно, что из вычислимости функции F следует вычислимость функции G. Кроме того, справедливо соотношение для любых X ΠN0: G(X) определена Û FX(X) не определена.

Предположим теперь, что функция G вычислима. Тогда существует число M, такое, что G = FM. Тогда имеем M ΠWM Û G(M) определено Û FM(M) не определено Û M Ï WM. Получили противоречие, и поэтому G — невычислима и, следовательно, F — невычислима, что и требовалось доказать.

Следствие 16.4. («Проблема применимости») Проблема «FX(Y) определена», X, Y ΠN0 — неразрешима.

Доказательство. Если бы данная проблема была разрешима, то и проблема «N ΠWN» была бы разрешима, что и требовалось доказать.

Рассмотрим теперь алгоритмический прием, позволяющий эффективно работать с номерами частично рекурсивных функций. Пусть F(X, Y) — вычислимая функция. Фиксируем X = A и положим GA(Y) = F(A, Y). Функция GA(Y) — одноместная и вычислимая. Значит, существует номер E такой, что GA(Y) = FE(Y) в последовательности (2). Покажем, что данный номер E находится эффективно.

Теорема 16.5. Для всякой вычислимой функции F(X, Y) существует общерекурсивная функция S(X) такая, что F(X, Y) = FS(X)(Y).

Доказательство. Пусть F — программа МПД, вычисляющая F(X, Y). Фиксируем X = A, и рассмотрим программу МПД QA, где

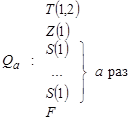
Легко убедиться, что данная программа QA вычисляет F(A, Y). Пусть S(A) — номер программы QA. Согласно построению F(A, Y) = FS(A)(Y). При этом, поскольку F фиксирована, то S(A) — эффективно вычислима, что и требовалось доказать.

Теперь, в силу вычислимости F(X, Y) существует N такое, что F(X, Y) = U(2)(N, X, Y), где U(2) — универсальная функция для двухместных частично рекурсивных функций. Тогда в предыдущей конструкции при X = A имеем S = S(N, A) и выполнено FS(N, A)(Y) = = U(S(N, A), Y), где U — универсальная для одноместных частично рекурсивных функций. Таким образом, используя тезис Черча и приведенную выше конструкцию, установлена теорема.

Теорема 16.6 (нумерационная). Существует общерекурсивная функция S(N, X) такая, что выполнено

U(2)(N, X, Y) = U(S(N, X), Y).

Данная теорема справедлива и в более общей ситуации, которую отметим без доказательства.

Теорема 16.7. Для любых M, N ³ 1 существует общерекурсивная функция , такая, что выполнено

,

Где K ΠN0, , .

Данное утверждение называют S-M-N-теоремой.

Теорема 16.8. Проблема «FX = », X ΠN0 — неразрешима. (Здесь означает функцию, тождественно равную нулю.)

Доказательство. Рассмотрим следующую функцию:

Легко видеть, что функция F(X, Y) вычислима, поскольку универсальная функция U(N, X) вычислима. По теореме 16.5 существует общерекурсивная функция S(X) такая, что F(X, Y) = FS(X)(Y) = = U(S(X), Y). Имеем по определению X ΠWX Û FS(X)(Y) = . Если бы проблема FZ(Y) = , Z ΠN0 была разрешима, то тогда проблема «X ΠWX» была бы разрешимой, что противоречило бы теореме 16.3, что и требовалось доказать.

Следствие16.9. Проблема «FX = FY», X, Y Î N0 — неразрешима.

Теорема 16.10 (Клини). Для любой частично рекурсивной функции H(X) существует число А такое, что FH(A)(X) = FA(X).

Доказательство. Пусть задана частично рекурсивная функция H(X). Рассмотрим вспомогательную функцию F(Y, X) = U(H(S(Y, Y)), X), где S — функция из тождества (10), существующая по нумерационной теореме 16.6. Поскольку функция F(Y, X) — частично рекурсивная, то существует число N, такое, что F(Y, X) = U(H(S(Y, Y)), X) = = U2(N, Y, X). По нумерационной теореме 16.6 имеем F(Y, X) = = U(S(N, Y), X) или U(H(S(Y, Y)), X) = U(S(N, Y), X). Теперь положим Y = N, и поскольку функция S общерекурсивна, то S(N, N) определено. Тогда получаем U(H(S(N, N)), X) = U(S(N, N), X). Обозначая S(N, N) = A, имеем U(H(A), X) = U(A, X) или FH(A)(X) = FA(X), что и требовалось доказать.

Теперь используем полученные результаты для установления фундаментального факта, полученного Райсом, показывающего, что проблема проверки любого нетривиального свойства частично рекурсивных функций неразрешима.

Произвольное множество А Í N0 называется Рекурсивным, если соответствующая характеристическая функция , где

Вычислима. Ясно, что рекурсивное множество А характеризуется тем, что проблема «X ΠA» разрешима. Пусть F — множество одноместных частично рекурсивных функций, отличных от пустого множества и от множества всех одноместных частично рекурсивных функций (т. е. F — нетривиальное множество). Обозначим через NF — множество всех номеров функций из F.

Теорема 16.11. (Райс) Множество NF нерекурсивно.

Доказательство. Предположим, что множество NF рекурсивно. Тогда его дополнение также рекурсивно, так как . По условию оба множества NF и непустые. Выберем некоторые a Î NF и b Π и определим функцию

Функция G(X) общерекурсивна, так как выполнено равенство G(X) = a + b. По теореме 16.10 для функции G(X) существует число А такое, что FG(A)(X) = FA(X). Тогда должно быть либо A ΠNF, либо A Î . Если A ΠNF, то, по определению, FA ΠF, и так как FG(A) = FA, то FG(A) ΠF. Однако из A ΠNF следует G(A) = = b Î , т. е. G(A) Î , и тогда FG(A) Ï F. Получено противоречие.

Если A Î , то, по определению, FA Ï F и тогда в силу FG(A) = FA имеем FG(A) Ï F. Однако из A Î имеем G(A) = a ΠNF, т. е. G(A) Î NF и значит FG(A) ΠF. Снова получено противоречие.

Итак, число А не содержится ни в одном из множеств NF и , чего быть не может, так как N0 = NF È . Противоречие является следствием предположения о рекурсивности множества NF, что и требовалось доказать.

Пусть Q — некоторое нетривиальной свойство одноместных частично рекурсивных функций, т. е. имеются функции как обладающие свойством Q, так и не обладающие свойством Q.

Теорема 16.12. Проблема «F обладает свойством Q», F ΠE1 неразрешима.

Доказательство. Пусть проблема «F обладает свойством Q», F ΠE1 разрешима, т. е. существует МПД, которая для любой F ΠE1 начальную конфигурацию (N, 0, …), где N — номер функции F, через конечное число шагов переводит в заключительную конфигурацию (1, *, …), если F обладает свойством Q, и в заключительную конфигурацию (0, *, …), если F не обладает свойством Q. Тогда для множества номеров функций из E1, обладающих свойством Q, можно указать разрешающую процедуру для проблемы N Î соотношением N Î Û МПД дает результат 1.

Данное соотношение показывает, что множество рекурсивно, что противоречит теореме 16.11, что и требовалось доказать.

Теорема 16.11 имеет многочисленные применения в теоретическом программировании и позволяет доказывать неразрешимость многих задач, связанных с вычислением на машинах. Большое число алгоритмически неразрешимых проблем имеется в книге: Роджерс Х. Теория рекурсивных функций и эффективная вычислимость. М., 1972.

Приведем одно важное понятие теории алгоритмов, связанное с вычислимостью. Выше была установлена невычислимость характеристической функции предиката «X ΠWX». В то же время частичная характеристическая функция, определенная соотношением

Является вычислимой. Это следует из тезиса Черча. Поэтому говорят, что проблема «X ΠWX» Полувычислима.

Многие проблемы, будучи неразрешимыми, являются полувычислимыми.

Определение 16.13. Предикат М() на натуральных числах (здесь ) называется Полувычислимым, если частичная характеристическая функция F, определенная соотношением

Вычислима.

Замечание 16.14. В литературе также используются равносильные термины: частичная разрешимость, рекурсивная перечислимость.

Примеры:

1. Любой разрешимый предикат полувычислим.

2. Для любой вычислимой функции G() проблема «Î D(G)» является полувычислимой, так как вычислима функция (здесь ).

3. Проблема «X Ï WX» не является полувычислимой. Действительно, если F — соответствующая частичная характеристическая функция, то . Значит, D(F) отличается от области определения любой одноместной вычислимой функции. Поэтому F не может быть вычислимой.

Теорема 16.15. Предикат М() полувычислим тогда и только тогда, когда существует вычислимая функция G() такая, что

М() = и Û Î D(G).

Доказательство. Если М() полувычислим и F — соответствующая частичная характеристическая функция, то по определению М() = и Û Î D(G). Обратное следует из примера 2.

Определение 16.16. Множество А из N0 называется Рекурсивно перечислимым, если частичная характеристическая функция F, где

Вычислима. Это равносильно тому, что предикат «X ΠA» полувычислим.

Теорема 16.16 может быть перефразирована следующим образом: Множество является рекурсивно перечислимым тогда и только тогда, когда оно является областью определению одноместной вычислимой функции.

< Предыдущая		Следующая >