15.1. Нумерация МПД-программ

Приведем аналогичную конструкцию по нумерации МПД-программ, которая позволит получить нумерацию МПД-вычислимых функций. Сначала определим нумерацию команд. Положим

A(Z(N)) = 4×(N – 1),

A(S(N)) = 4×(N – 1) + 1,

A(T(M, N)) = 4×P(M – 1, N – 1) + 2,

A(J(M, N, Q)) = 4×p(M, N, Q) + 3,

Где P(X, Y) = 2X×(2Y + 1) – 1, p(X, y, Z) = P(P(X – 1, Y – 1), Z – 1).

Ясно, что функция a эффективно вычислима. Для вычисления действуем так:

Находим числа U, V, такие, что X = 4U + V, где . Тогда имеем:

 = Z(U + 1), если V = 0;

= S(U + 1), если V = 1;

= T(L(U) + 1, R(U) + 1), если V = 2;

= J(M, N, Q), если V = 3, где (M, N, Q) = .

Следовательно, функция также эффективно вычислима.

Пусть теперь дана МПД-программа P = I1. . .IS. Определим ее номер g(Р) = t(a(I1), …, a(IS)), где

T(X1, …, XS) = .

Ясно, что тем самым определена биекция g множества программ в множество натуральных чисел, причем функции g и g-1 эффективно вычислимы, по программе Р эффективно находится ее номер N = g(P), а по номеру N можно эффективно найти программу Р такую, что N = g(P). Число g(P) называется номером программы Р. Например, если Р = I1I2I3, где I1 = T(3, 1), I2 = S(4), I3 = Z(6), то

A(T(3, 1)) = 18, a(S(4)) = 13, a(Z(6)) = 20.

Следовательно, g(P) = 218232253 – 1. Пусть теперь дано N = 4127. Поскольку 4127 = 25 + 212 – 1, то Р = I1I2, где a(I1) = 5, a(I2) = = 18 – 5 – 1. Следовательно, I1 = S(2), I2 = T(2, 1).

Разумеется, существуют и другие способы нумерации программ, для нас важна лишь эффективная вычислимость функций g и g-1.

Таким образом, получаем эффективную нумерацию МПД-программ:

P0, P1, P2, …, PN, … .

Теперь, имея нумерацию МПД-программ, можно занумеровать МПД-вычислимые функции. Для любого A ΠN и N ³ 1 определим N-местная функция, вычислимая программой с номером А. Это дает нумерацию N-местных МПД-вычислимых функций , , , …

Например, если А = 4127, то согласно определению имеем:

, N = 1;

, N > 1.

Поскольку для всякой частично рекурсивной функции существует вычисляющая ее МПД-программа Р, то , где A = g(P). Число А называют номером (индексом) функции .

Приведем одно применение существования нумерации частично рекурсивных функций.

Теорема 15.2. Существует всюду определенная функция, не являющаяся частично рекурсивной.

Доказательство. Построим всюду определенную функцию j, отличающуюся от каждой частично рекурсивной функции F0, F1, …, FN, … в перечислении одноместных частично рекурсивных функций. Полагаем

Функция j всюду определена и отличается от FN при X = N, N ΠN0. Действительно, если FN(N) определено, то j(N) = FN(N) + 1, если FN(N) не определено, то j(N) определено и равно 0. Поскольку j отличается от FN при всех N ΠN0, то j не может находиться в перечислении (10) и, значит, она не может быть частично рекурсивной, что и требовалось доказать.

Замечание. 15.3. Приведенный метод рассуждения есть пример диагональной конструкции Кантора, с помощью которой им была доказана несчетность множества действительных чисел. Данным методом можно установить нерекурсивность большого класса функций.

Например, функция

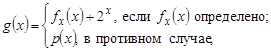
Причем P(X) — целочисленный полином является всюду определенной и не частично рекурсивной.

< Предыдущая		Следующая >