13. Нумерация наборов чисел и слов

В теории алгоритмов получил распространение прием, позволяющий сводить изучение функций от нескольких переменных к изучению функций одной переменной. Он основан на нумерации наборов чисел так, что имеется биективное соответствие между наборами чисел и их номерами, причем функции, определяющие по набору чисел его номер и по номеру сам набор чисел являются общерекурсивными.

Рассмотрим сначала множество  — множество пар натуральных чисел. Рассмотрим следующее упорядочение этих пар, называемой Канторовским:

(0, 0), (0, 1), (1, 0), (0, 2), (1, 1), (2, 0), … (13.1)

Здесь в порядке возрастания упорядочиваются пары (X, Y) с условием X + Y = N в виде последовательности

(0, N), (1, N – 1), …, (X, Y), …, (N, 0). (13.2)

Пусть C(X, Y) — номер пары (X, Y) в последовательности (13.1), причем считаем C(0, 0) = 0. Если C(X, Y) = N, то обозначим через R, L — функции, удовлетворяющие X = L(N), Y = R(N) и, следовательно, C(L(N), R(N)) = N.

Покажем, что функции C, L, R в явном виде выражаются через обычные арифметические функции. Произвольная пара (X, Y) находится на месте X + 1 в последовательности (13.2). Далее, перед последовательностью (13.2) находятся последовательности, отвечающие элементам (X, Y) с условием X1 + Y1 = T, где T = 0, 1, …, X + Y – 1, и каждая из них содержит T + 1 элемент.

Следовательно, элемент (X, Y) находится в последовательности (13.1) на месте 1 + 2 + … + X + Y + X + 1. Поскольку нумерация начинается с нуля, то номер элемента (X, Y) в последовательности (13.1) равен

. (13.3)

Пусть теперь C(X, Y) = N и найдем X = L(N) и Y = R(N). Из (13.3) следуют равенства:

;

;

.

Следовательно, или

.

Это означает, что

. (13.4)

Теперь, используя (13.3), определяем X:

.

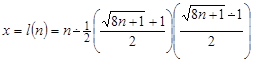Подставляя найденное значение X в (13.4), получаем Y:

.

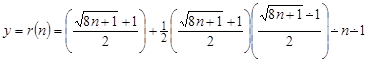Заметим, что важен не сам вид полученных функций C(X, Y), R(N), L(N), а важен факт их эффективной вычислимости.

Теперь с помощью нумерации пар чисел легко получить нумерацию троек чисел, т. е. элементов множества . Определим функцию . Тогда, если , то Z = R(N), Y = R(L(N)), X = L(L(N)).

Аналогично, для наборов произвольной длины R + 1 полагаем

, , …,

…

И по определению называем число канторовским номером N-ки . Если , то XN = R(M), XN – 1 = R(L(M)), …, X2 = R(L(…L(M)), X1 = L(L(…L(M)).

Теперь, имея нумерацию множеств (K > 0), можно установить нумерацию множества . Положим для любого . Ясно, что С — биективное соответствие между М и N0. Кроме того, если , то , . Отсюда эффективно определяются .

Приведем еще одну нумерацию наборов чисел. Номер пары (X, Y) зададим функцией

.

Ясно, что это общерекурсивная функция. При этом, если P(X, Y) = N, то выполнено , . Следовательно, для данной нумерации , .

Теперь, имея нумерационную функцию для пар чисел, аналогично предыдущему строим нумерационные функции для К-ок чисел и множества наборов .

Другую нумерацию множества М можно получить так. Пусть

.

Ясно, что  — вычислима. Чтобы установить вычислимость , заметим, что каждое натуральное число имеет единственное представление в двоичной позиционной записи. Т. е. для любого N можно эффективно и однозначно найти K > 0 и такое, что . Откуда получаем , где , (0 < I < K).

Рассмотрим теперь вопрос о нумерации слов в некотором алфавите и укажем некоторые из применяемых способов такой нумерации.

Пусть  — конечный алфавит и пусть  — множество всех слов конечной длины в алфавите А, включая и пустое слово ^.

Алфавитная нумерация определяется следующим образом:

C(^) = 0, .

Поскольку при фиксированном R каждое положительное число N однозначно представимо в виде

, (0 < IJ < R + 1),

То каждое число есть алфавитный номер одного и только одного слова из множества . Разложение (16) называется R-ичным разложением числа N с цифрами 1, …, R в отличии от обычного R-ичного разложения с коэффициентами 0, …, R – 1.

Нумерация слов через нумерационные функции. Пусть имеется счетный алфавит . Тогда нумерация слов определяется так:

V(^) = 0, ,

Где функция определена выше. Ясно, что так определенная функция V является биективной и вычислимой.

Геделевская нумерация. Пусть имеем счетный алфавит . Определим Геделевы номера для каждой буквы . Теперь для каждого слова определим геделев номер , где  — K-е простое число. Кроме того, положим G(^) = 1. При этом геделев номер последовательности слов P0, P1, …, PK определяется так: .

Рассмотрим теперь два применения нумерационных функций.

Утверждение 13.1. а) Функция F(X, Y), отличная от нуля на конечном множестве пар из , общерекурсивна.

Доказательство. Действительно, пусть на парах чисел и пусть имеет на них значения Z1, …, ZT. На остальных пара F(X, Y) = 0. Положим , где C — нумерационная функция Кантора.

Определим функцию G так: , G(U) = 0 на остальных . Было выше показано, что G — общерекурсивна. По построению выполнено F(X, Y) = G(C(X, Y)) и поэтому F — общерекурсивна.

Б) Определим сначала понятие Совместной рекурсии. В схеме совместной рекурсии функция порождается с помощью нескольких функций.

Пусть для определенности даны функции , , здесь . Тогда можно определить пару функций и по рекурсии:

,

,

,

.

Утверждение 13.2. Если G1, G2, H1, H2 — общерекурсивные функции, то F1, F2 также общерекурсивны.

Доказательство. Определим функцию

,

Где C — нумерационная функция Кантора. Тогда имеем: , . Далее имеем

—

Частично рекурсивная по условию.

Т. е. функция получается по схеме обычной рекурсии с помощью функций

,

.

Значит функция  — частично рекурсивная, а потому частично рекурсивны и функции и , что и требовалось доказать.

< Предыдущая		Следующая >