11.3. Машины произвольного доступа и вычислимые функции
Опишем другую алгоритмическую модель, представляющую собой идеализированную ЭВМ и предложенную в 70-х годах XX века с целью моделирования реальных вычислительных машин и анализа сложности вычислений.
Машина произвольного доступа (МПД) состоит из бесконечного числа регистров R1, R2, …, в каждом из которых может быть записано натуральное число из ![]() . Пусть
. Пусть ![]() есть число, записанное в регистре
есть число, записанное в регистре ![]() ,
, ![]() . Состоянием машины или Конфигурацией назовем последовательность чисел
. Состоянием машины или Конфигурацией назовем последовательность чисел ![]() . Функционирование машины заключается в изменении конфигураций путем выполнения Команд в порядке их написания.
. Функционирование машины заключается в изменении конфигураций путем выполнения Команд в порядке их написания.
Машина имеет следующие типы команд.
Команды обнуления. Для всякого ![]() имеется команда
имеется команда ![]() . Действие команды
. Действие команды ![]() заключается в замене содержимого регистра
заключается в замене содержимого регистра ![]() на 0. Содержимое других регистров не меняется. Обозначение действия
на 0. Содержимое других регистров не меняется. Обозначение действия
![]() :
:
![]() := 0.
:= 0.
Команды прибавления единицы. Для всякого ![]() имеется команда
имеется команда ![]() . Действие команды
. Действие команды ![]() заключается в увеличении содержимого регистра
заключается в увеличении содержимого регистра ![]() на 1. Содержимое других регистров не меняется. Обозначение действия
на 1. Содержимое других регистров не меняется. Обозначение действия ![]() :
:
![]() :=
:= ![]() + 1.
+ 1.
Команды переадресации. Для всех ![]() имеется команда
имеется команда ![]() . Действие команды
. Действие команды ![]() заключается в замене содержимого регистра
заключается в замене содержимого регистра ![]() числом
числом ![]() — хранящимся в регистре
— хранящимся в регистре ![]() . Содержимое других регистров не меняется (включая и
. Содержимое других регистров не меняется (включая и ![]() ). Обозначение действия
). Обозначение действия ![]() :
:
![]() :=
:=![]() или
или ![]() à
à ![]() .
.
Команды условного перехода. Для всяких ![]() имеется команда
имеется команда ![]() . Действие этой команды заключается в:
. Действие этой команды заключается в:
Сравнении содержимого регистров ![]() и
и ![]() , затем:
, затем:
А) если ![]() =
= ![]() , то МПД переходит к выполнению команды с номером (идентификатором) Q в списке команд;
, то МПД переходит к выполнению команды с номером (идентификатором) Q в списке команд;
B) если ![]() ¹
¹ ![]() , то МПД переходит к выполнению следующей команды в списке команд.
, то МПД переходит к выполнению следующей команды в списке команд.
Конечная, упорядоченная последовательность команд данных типов составляет Программу МПД.
Пусть зафиксирована начальная конфигурация ![]() чисел и программа
чисел и программа ![]() . Тогда однозначно определена последовательность конфигураций
. Тогда однозначно определена последовательность конфигураций ![]() , где
, где ![]() есть конфигурация, полученная из конфигурации
есть конфигурация, полученная из конфигурации ![]() применением команды
применением команды ![]() . Пусть на некотором шаге выполнена команда
. Пусть на некотором шаге выполнена команда ![]() и получена конфигурация
и получена конфигурация ![]() . Тогда, если
. Тогда, если ![]() не есть команда условного перехода, то следующая конфигурация
не есть команда условного перехода, то следующая конфигурация ![]() есть конфигурация, полученная из
есть конфигурация, полученная из ![]() применением команды
применением команды ![]() . Если
. Если ![]() есть команда условного перехода, т. е. IT = J(M, N, Q), то
есть команда условного перехода, т. е. IT = J(M, N, Q), то ![]() получается из
получается из ![]() применением команды
применением команды ![]() , если
, если ![]() =
= ![]() в конфигурации
в конфигурации ![]() и команды
и команды ![]() , если
, если ![]() ¹
¹![]() . Последовательность конфигураций будет обозначаться также P(A1, A2, …) или
. Последовательность конфигураций будет обозначаться также P(A1, A2, …) или ![]() и называться Вычислением.
и называться Вычислением.
Вычисление (работа машины) останавливается, если:
Выполнена последняя команда, т. е. T = S И ![]() не есть команда условного перехода;
не есть команда условного перехода;
Если IT = J(M, N, Q), ![]() =
= ![]() в конфигурации
в конфигурации ![]() и Q > S;
и Q > S;
Если IT = J(M, N, Q), ![]() ¹
¹ ![]() в конфигурации
в конфигурации ![]() и T = S.
и T = S.
Если вычисление остановилось, то последовательность ![]() содержимого регистров
содержимого регистров ![]() называется Заключительной конфигурацией. Если последовательность
называется Заключительной конфигурацией. Если последовательность ![]() конечна, то говорим, что МПД применима к начальной конфигурации
конечна, то говорим, что МПД применима к начальной конфигурации ![]() и пишем P(A1, A2, …)¯ или
и пишем P(A1, A2, …)¯ или ![]() . В противном случае говорим, что МПД неприменима к
. В противном случае говорим, что МПД неприменима к ![]() и пишем P(A1, A2, …) или
и пишем P(A1, A2, …) или ![]() .
.
Будем рассматривать только такие начальные конфигурации, в которых имеется конечное число элементов, отличных от нуля. Будем писать ![]() вместо
вместо ![]() для таких конфигураций. Ясно, что любого T конфигурация
для таких конфигураций. Ясно, что любого T конфигурация ![]() будет содержать конечное число отличных от нуля элементов, если этим свойством обладает конфигурация
будет содержать конечное число отличных от нуля элементов, если этим свойством обладает конфигурация ![]() .
.
Теперь условимся, что понимать под вычислением функций на МПД. Рассмотрим частичные функции F типа ![]() . Пусть
. Пусть ![]() — фиксированная программа. Пусть
— фиксированная программа. Пусть ![]() . Будем говорить, что вычисление дает результат B, если
. Будем говорить, что вычисление дает результат B, если ![]() и в заключительной конфигурации
и в заключительной конфигурации ![]() . Обозначение:
. Обозначение: ![]() . Будем говорить, что программа Р вычисляет функцию F, если для любых
. Будем говорить, что программа Р вычисляет функцию F, если для любых ![]() выполнимо
выполнимо
![]() .
.
Назовем функцию F вычислимой (на МПД), если существует программа Р, которая вычисляет F. Класс вычислимых (на МПД) функций обозначим Е.
Заметим, что любая программа Р для любого N ³ 1 на начальных конфигурациях вида ![]() определяет N-местную частичную функцию
определяет N-местную частичную функцию ![]() , такую, что для всех
, такую, что для всех ![]()
![]()
Ясно, что разные программы могут вычислять одну и ту же функцию.
Распространим понятие алгоритмической вычислимости на предикаты, заданные на множестве ![]() . Пусть
. Пусть ![]() — произвольный такой предикат. Определим характеристическую функцию
— произвольный такой предикат. Определим характеристическую функцию ![]() предиката p соотношением:
предиката p соотношением:
![]()
Будем называть предикат p разрешимым, если его характеристическая функция вычислима, и не разрешимым в противном случае.
Это понятие соответствует вопросу о наличии алгоритма для проверки свойства, определяемого предикатом.
Теперь распространим понятие вычислимости на функции, отличные от рассматриваемого типа.
Пусть D — некоторое множество, и ![]() — функция от N переменных. Зафиксируем эффективное кодирование множества D натуральными числами
— функция от N переменных. Зафиксируем эффективное кодирование множества D натуральными числами ![]() , т. е. зададим инъективную функцию
, т. е. зададим инъективную функцию ![]() . Пусть
. Пусть ![]() — ее обратная. Тогда для функции
— ее обратная. Тогда для функции ![]() можно однозначно определить функцию
можно однозначно определить функцию ![]() , где
, где ![]() или
или
![]() ,
,
Для любых ![]() .
.
Будем называть функцию F вычислимой тогда и только тогда, когда функция F* вычислима.
Пример 11.1. Кодирование множества целых чисел Z. Пусть
![]()
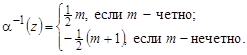
Таким образом, можно считать определенным понятие вычислимости целочисленных функций. Позднее будут рассмотрены эффективные кодирования и других областей.
Рассмотрим примеры вычислимых функций (на МПД).
А) Функция F(X, Y) = X + Y. Эта функция может быть вычислена следующей программой при начальной конфигурации (X, Y, 0, 0, …). P = I1 I2 I3 I4, где I1 = J(3, 2, 5), I2 = S(1), I3 = S(3), I4 = J(1, 1, 1). Данная программа прибавляет 1 к X до тех пор, пока R3 не станет равным Y.
B) Функция ![]()
Эта функция может быть вычислена программой Р = I1 I2 I3 I4 I5 I6, где I1 = J(1, 2, 6), I2 = S(3), I3 = S(2), I4 = S(2), I5 = J(1, 1, 1), I6 = T(3, 1).
Данная программа прибавляет 1 к R3 и 2 к R2 до тех пор, пока R2 не станет равным X, тогда R3 даст результат.
Поскольку доказательства вычислимости конкретных функций связаны с предъявлением конкретных программ, их вычисляющих, то следует ввести некоторые соглашения о составлении и записи программ. Аналогично композиции машин Тьюринга можно ввести композицию программ МПД.
Пусть ![]() . Будем говорить, что Р имеет стандартный вид, если для всякой команды условного перехода J(M, N, Q) выполнимо
. Будем говорить, что Р имеет стандартный вид, если для всякой команды условного перехода J(M, N, Q) выполнимо ![]() . Две программы Р и
. Две программы Р и ![]() назовем эквивалентными, если они определяют одни и те же N-местные функции, т. е.
назовем эквивалентными, если они определяют одни и те же N-местные функции, т. е. ![]() для всех
для всех ![]() .
.
Утверждение 11.2. Для всякой программы Р существует эквивалентная ей программа стандартного вида ![]() .
.
Доказательство. Пусть ![]() . Тогда определим
. Тогда определим ![]() где для любого
где для любого ![]()
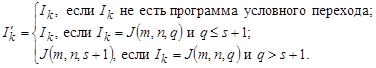 .
.
Ясно, что ![]() удовлетворяет нужным требованиям, что требовалось доказать.
удовлетворяет нужным требованиям, что требовалось доказать.
Пусть теперь даны две программы P и Q стандартного вида. Образуем программу ![]() (где
(где ![]() ,
, ![]() ) с учетом нумерации, т. е. команды J(M, N, Q) заменены на J(M, N, S + Q). Тогда результат действия программы PQ совпадает с результатом вычисления по программе P, к которому применена программа Q.
) с учетом нумерации, т. е. команды J(M, N, Q) заменены на J(M, N, S + Q). Тогда результат действия программы PQ совпадает с результатом вычисления по программе P, к которому применена программа Q.
Заметим, что для всякой программы Р существует минимальное натуральное число R(P) такое, что для всех ![]() , входящих в команды из Р, т. е. S(N), Z(N), T(M, N), J(M, N, Q) выполнено M, N < R(P). Это число иногда называют Ширина, ранг программы Р.
, входящих в команды из Р, т. е. S(N), Z(N), T(M, N), J(M, N, Q) выполнено M, N < R(P). Это число иногда называют Ширина, ранг программы Р.
Смысл числа R(P) состоит в том, что регистры ![]() с T > R(P) в ходе вычисления по программе Р не будут менять свое содержание и не будут влиять на содержимое регистров
с T > R(P) в ходе вычисления по программе Р не будут менять свое содержание и не будут влиять на содержимое регистров ![]() , поэтому их можно использовать для других вычислений.
, поэтому их можно использовать для других вычислений.
Заметим также, что можно организовывать вычисление, используя программу Р, в случае, когда входы программы находятся в регистрах ![]() , а результат заносится в
, а результат заносится в ![]() . Далее для простоты положим, что регистры
. Далее для простоты положим, что регистры ![]() отличны от
отличны от ![]() .
.
Пусть Р вычисляет F в стандартном понимании вычислимости. Тогда программа
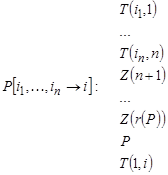
Будет вычислять ![]() и результат запишет в
и результат запишет в ![]() . Данную программу обозначим
. Данную программу обозначим ![]() .
.
Пример 11.3. Функция F(X, Y) = Xy — вычислимая функция. Пусть Н — программа, вычисляющая функцию X + Y (пример а) ). Тогда ![]() вычисляется программой
вычисляется программой
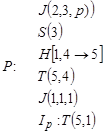
Программа Р вычисляет Xy по правилу ![]()
Как следует из изложенного, язык программ МПД содержит основные процедуры языков программирования и позволяет устраивать композицию (соединение) программ и использовать программы в качестве подпрограмм других программ. Это является основанием для предположения о том, что введенный класс вычислимых функций в точности отвечает классу алгоритмически вычислимых функций. Данное предположение называется Тезисом Черча (для МПД). Так же как и тезис Тьюринга, данный тезис доказать нельзя, однако принятие его позволяет истолковывать утверждения о несуществовании МПД для решения конкретных задач как утверждения о несуществовании алгоритмов вообще.
| < Предыдущая | Следующая > |
|---|