01.2. Геометрический способ задания
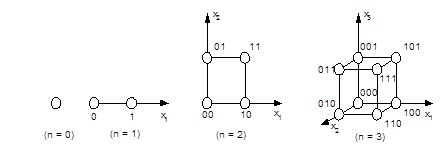
Под геометрическим способом задания двоичной функции F(X1, ..., XN) понимается выделение тех вершин N-мерного двоичного куба, на наборах координат которых функция принимает единичное значение. На рис.1.1 приведены двоичные кубы размерностей N = 0, 1, 2, 3.
Рис.1.1
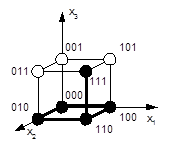
Выделим среди множества вершин N-мерного куба те, на наборе координат которых функция принимает единичное значение. Например, функции, заданной табл.1.5 соответствует геометрическое задание, изображенное на рис.1.2.
Таблица 1.5
|
X1 |
X2 |
X3 |
F |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
|
|
|
|
Рис.1.2 |
Рис.1.3 |
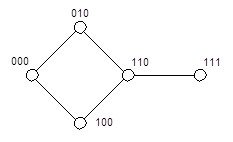
Часто по геометрическому заданию функции строят Граф связности вершин n-мерного куба, соответствующий данной функции. Для этого сначала отмечают те ребра, у которых оба конца выделены, т. е. соответствующие вершины лежат в области истинности. Затем все остальные ребра и вершины, не лежащие в области истинности, отбрасывают. Так функции, изображенной на рис.1.2, соответствует граф связанности, приведенный на рис.1.3.
| < Предыдущая | Следующая > |
|---|