68. Рассмотрим некоторые примеры линейных операторов

Оператор Проектирования. Пусть требуется найти матрицу линейного оператора, осуществляющего проектирование трехмерного пространства на координатную ось Е1 в базисе Е1, Е2, Е3. Матрица линейного оператора – это матрица, в столбцах которой должны стоять образы базисных векторов Е1 = (1,0,0), Е2 = (0,1,0), Е3 = (0,0,1). Эти образы, очевидно, есть: Ае1 = (1,0,0)

Ае2 = (0,0,0)

Ае3 = (0,0,0)

Следовательно, в базисе Е1, Е2, Е3 матрица искомого линейного оператора будет иметь вид: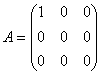

Найдем ядро этого оператора. Согласно определению ядро – это множество векторов Х, для которых АХ = 0. Или

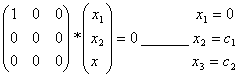
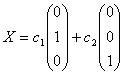
Т. е. ядро оператора составляет множество векторов, лежащих в плоскости Е1, Е2. Размерность ядра равна n – rangA = 2.

Множество образов этого оператора – это, очевидно, множество векторов, коллинеарных Е1. Размерность пространства образов равна рангу линейного оператора и равна 1, что меньше размерности пространства прообразов. Т. е. оператор А – вырожденный. Матрица А тоже вырождена.

Еще пример: найти матрицу линейного оператора, осуществляющего в пространстве V3 (базис I, J, K) линейное преобразование – симметрию относительно начала координат.

Имеем: Ai = - i

Aj = - j

Ak = - k

Т. е. искомая матрица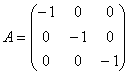

Рассмотрим линейное преобразование – Симметрию относительно плоскости Y = X.

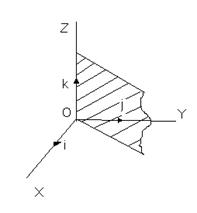
Ai = j (0,1,0)

Aj = I (1,0,0)

Ak = K (0,0,1)

Матрица оператора будет:

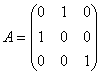
Ai Aj Ak

 

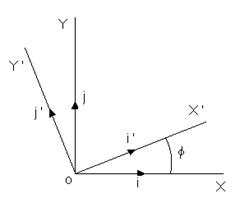Еще пример – уже знакомая матрица, связывающая координаты вектора при повороте осей координат. Назовем оператор, осуществляющий поворот осей координат, - оператор поворота. Допустим, осуществляется поворот на угол j:

Ai ’ = cosjI + sinjJ

Aj ’ = - sinjI + cosjJ

Матрица оператора поворота:

Ai ‘ Aj ‘

Вспомним формулы преобразования координат точки при смене базиса – замена координат на плоскости при смене базиса:

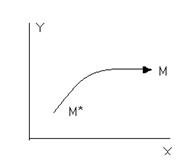Эти формулы можно рассматривать двояко. Ранее мы рассматривали эти формулы так, что точка стоит на месте, поворачивается координатная система. Но можно рассматривать и так, что координатная система остается прежней, а перемещается точка из положения М* в положение М. Координаты точки М и М* определены в той же координатной системе.

 

 

 

 

 

Все сказанное позволяет подойти к следующей задаче, которую приходится решать программистам, занимающимся графикой на ЭВМ. Пусть необходимо на экране ЭВМ осуществить поворот некоторой плоской фигуры (например треугольника) относительно точки О’ с координатами (a, b) на некоторый угол j. Поворот координат описывается формулами:

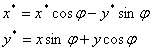
Параллельный перенос обеспечивает соотношения:

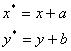
Для того, чтобы решить такую задачу, обычно применяют искусственный прием: вводят так зазываемые “однородные” координаты точки на плоскости XOY: (x, y, 1). Тогда матрица, осуществляющая параллельный перенос, может быть записана:

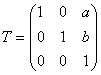
Действительно:

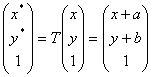
А матрица поворота:

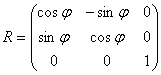
Рассматриваемая задача может быть решена в три шага:

1й шаг: параллельный перенос на вектор А(-а, - b) для совмещения центра поворота с началом координат:

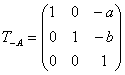
2й шаг: поворот на угол j:

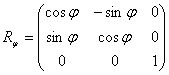
3й шаг: параллельный перенос на вектор А(а, b) для возвращения центра поворота в прежнее положение:

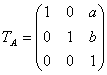
Искомое линейное преобразование в матричном виде будет выглядеть:

(**)

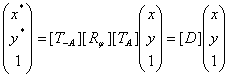Где

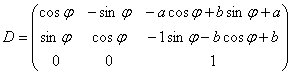
По формуле (**) можно пересчитать координаты любой точки плоской фигуры, а затем построить ее на экране, осуществив тем самым ее поворот.

< Предыдущая		Следующая >