67. Линейные операторы в евклидовом пространстве

Пусть линейный оператор А действует в евклидовом пространстве En и преобразует это пространство само в себя.

Введем Определение: оператор А* назовем сопряженным оператору А, если для любых двух векторов X,Y из Еn выполняется равенство скалярный произведений вида:

(Ax,Y) = (X,A*Y)

Еще Определение: линейный оператор называется самосопряженным, если он равен своему сопряженному оператору, т. е. справедливо равенство:

(Ax,Y) = (X,Ay)

Или, в частности (Ax,X) = (X,Ax).

Самосопряженный оператор обладает некоторыми свойствами. Упомянем некоторые из них:

1. Собственные числа самосопряженного оператора - вещественны (без доказательства);

2. Собственные векторы самосопряженного оператора ортогональны. Действительно, если X1 и X2 – собственные векторы, а l1 и l2 – их собственные числа, то: Ax1 = l1X; Ax2 = l2X; (Ax1,X2) = (X1,Ax2), или l1(X1,X2) = l2(X1,X2). Поскольку l1 и l2 различны, то отсюда (X1,X2) = 0, что и требовалось доказать.

3. В евклидовом пространстве существует ортонормированный базис из собственных векторов самосопряженного оператора А. Т. е. матрицу самосопряженного оператора всегда можно привести к диагональному виду в некотором ортонормированном базисе, составленном из собственных векторов самосопряженного оператора.

Еще одно Определение: назовем самосопряженный оператор, действующий в евклидовом пространстве Симметричным оператором. Рассмотрим матрицу симметричного оператора. Докажем утверждение: чтобы оператор был симметричным, необходимо и достаточно, чтобы в ортонормированном базисе его матрица была бы симметричной.

Пусть А – симметричный оператор, т. е.:

(Ax,Y) = (X,Ay)

Если А – матрица оператора А, а X и Y – некоторые векторы, то запишем:

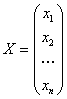
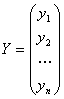координаты X и Y в некотором ортонормированном базисе

Тогда: (X,Y) = XTY = YTX и имеем (Ax,Y) = (AX)TY = XTATY

(X,Ay) = XT(AY) = XTAY,

Т. е. XTATY = XTAY. При произвольных матрицах-столбцах X, Y это равенство возможно только при АТ = А, а это означает, что матрица А – симметричная.

< Предыдущая		Следующая >