34. Плоскость. Различные ее виды

Прежде всего, в математике доказывается, что если в пространстве задана произвольная плоскость и декартова система координат, то уравнение этой плоскости является уравнением первой степени.

Мы докажем, что если в пространстве фиксирована произвольная система координат Oxyz, то всякое уравнение первой степени с тремя переменными x, y, z определяет относительно этой системы плоскость.

Доказательство: рассмотрим произвольное уравнение первой степени:

A X + B Y + C Z + D = 0,

Где хотя бы одно из A B C отлично от 0. Тогда это уравнение имеет хотя бы одно решение: к примеру A X0 + B Y0 + C Z0 + D = 0

Тогда вычитая одно из другого, получим эквивалентное уравнение:

A (X - X0) + B (Y - Y0) + C (Z - Z0) = 0. (*)

Для доказательства нашего утверждения достаточно доказать, что уравнение (*) определяет плоскость, проходящую через точку M(X0 Y0 Z0) и перпендикулярную вектору .

В самом деле, если точка M(X Y Z) лежит на указанной плоскости, то вектор ортогонален вектору и их скалярное произведение равно 0. Если же точка не лежит в указанной плоскости, то вектор не перпендикулярен И скалярное произведение не равно 0. Т. о. уравнение (*) (произвольное!) действительно определяет плоскость.

Уравнение A X + B Y + C Z + D = 0 называется общим уравнением плоскости, а вектор - нормальным вектором плоскости. Общее уравнение плоскости называется неполным, если какой-либо коэффициент может и не один, равен нулю. К примеру:

D = 0 : A x + B y + C z = 0

Определяет уравнение плоскости, проходящей через начало координат.

С = 0 : A X + B Y + D = 0 – плоскость, параллельная оси Z, так как -

A = 0 , B = 0 : C Z = 0 – плоскость, параллельная XOY и т. д. Всего 10 вариантов.

Если уравнение полное, то его можно свести к уравнению плоскости в отрезках:

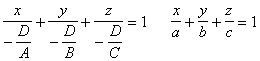
Ясно, что A, B, C – это отрезки, отсекаемые плоскостью на осях координат. Действительно, если Y = Z = 0, то X = A – определяет точку пересечения плоскости с OX.

< Предыдущая		Следующая >