33. Линии второго порядка
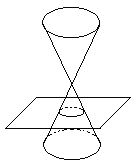 Линии второго порядка это эллипс, гипербола, парабола. Эти кривые представляют собой так называемые конические сечения. Это сечения конуса плоскостью. В зависимости от того, как проходит плоскость получается либо эллипс, либо парабола, либо гипербола. В механике линии второго порядка определяют траектории движения теля в поле центрального тяготения. Так, материальная точка (спутник) движется в поле тяготения Земли по эллипсу. Если его скорость равна второй космической, то по параболе, а если превысит вторую космическую – то по гиперболе.
Линии второго порядка это эллипс, гипербола, парабола. Эти кривые представляют собой так называемые конические сечения. Это сечения конуса плоскостью. В зависимости от того, как проходит плоскость получается либо эллипс, либо парабола, либо гипербола. В механике линии второго порядка определяют траектории движения теля в поле центрального тяготения. Так, материальная точка (спутник) движется в поле тяготения Земли по эллипсу. Если его скорость равна второй космической, то по параболе, а если превысит вторую космическую – то по гиперболе.
Общее уравнение кривой второго порядка – это полином второй степени:
A11 x2 + 2 a12 x y + a22 y2 + 2 a13 x + 2 a23 y + a33 = 0
В математике доказывается (мы этим займемся через несколько лекций), что путем преобразований координат – поворотов осей и переносов осей можно всегда данное уравнение привести к виду:
A11 x2 + a22 y2 = a33 Или y2= 2px
Такой вид уравнения кривой второго порядка называется каноническим.
Более того, доказывается также, что этими тремя линиями ( эллипс, парабола, гипербола) исчерпываются все линии второго порядка.
Рассмотрим в отдельности каждую кривую.
Каноническое уравнение эллипса. Эллипс получается, если плоскость пересекает Все образующие конуса.
 Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная. Очевидно, при совпадении точек F1 и F2 эллипс представляет собой окружность.
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная. Очевидно, при совпадении точек F1 и F2 эллипс представляет собой окружность.
Выведем каноническое уравнение эллипса: выберем начало координат в середине отрезка F1F2. Обозначим длину отрезка F1F2=2с, а расстояние, о котором мы говорили в определении эллипса – через 2а.
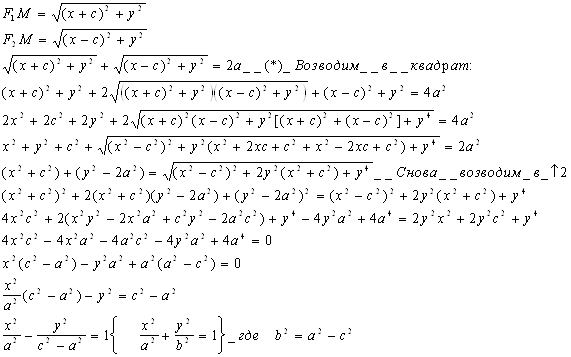
Лучше проделать следующие преобразования: умножим правую и левую части (*) на разность радикалов
![]() , сложим снова с (*) и возведем в квадрат
, сложим снова с (*) и возведем в квадрат
![]()
Отсюда ![]()
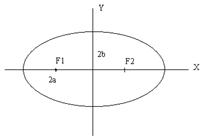 Величины a и b называются большой и малой полуосями соответственно. Строим эллипс:
Величины a и b называются большой и малой полуосями соответственно. Строим эллипс:
Каноническое уравнение гиперболы. Гипербола получается, когда плоскость пересекают образующие обеих полостей конуса.
Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная.
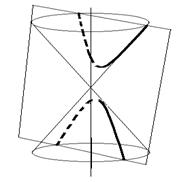 Выберем опять оси координат и начало координат посередине отрезка F1F2. Расстояние F1F2 равно 2с. А разность расстояний обозначим через 2а.
Выберем опять оси координат и начало координат посередине отрезка F1F2. Расстояние F1F2 равно 2с. А разность расстояний обозначим через 2а.
Аналогично предыдущему выводу уравнения эллмпса, имеем:

![]()
![]()
Преобразуем, как и ранее к виду:

Величины a и b называются действительной и мнимой полуосями гиперболы соответственно. Строим гиперболу:
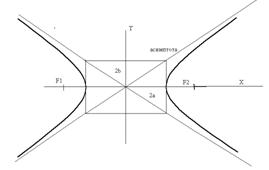 Сопряженная гипербола – ее ветви будут направлены вверх и вниз. Асимптоты гиперболы очевидно определяются уравнениями:
Сопряженная гипербола – ее ветви будут направлены вверх и вниз. Асимптоты гиперболы очевидно определяются уравнениями:
![]() 2а и 2в – действительная и мнимая оси гиперболы соответственно.
2а и 2в – действительная и мнимая оси гиперболы соответственно.
Каноническое уравнение параболы. Парабола получается, когда плоскость, пересекающая конус, параллельна одной из образующих. В механике космического полета существует так называемая параболическая скорость. Иначе еще она называется второй космической скоростью. Тело, имеющее вторую космическую скорость, движется по параболе, а если скорость больше – то по гиперболе.
Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фркусом параболы, а фиксированная прямая – директрисой параболы.
Для вывода уравнения построим:
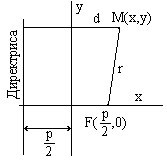 Согласно определению:
Согласно определению:

 Это и есть каноническое уравнение параболы. Параметр р называеся параметром параболы. К примеру, парабола y = x2: p=1/2
Это и есть каноническое уравнение параболы. Параметр р называеся параметром параболы. К примеру, парабола y = x2: p=1/2
Фокус – это точка F ( 0, 1/4), директриса y = - 1/4
Оказывается, директрису можно определить и для эллипса и для параболы. Заметим, что для параболы директрису можно определить и так: отношение расстояний от точки параболы до фокуса и до директрисы есть величина постоянная, равная единице. Для эллипса и гиперболы можно также ввести прямую, для которой отношение расстояний от некоторой точки эллипса или гиперболы до фокуса и до прямой, называемой тоже директрисой, есть величина постоянная.
Для выяснения этого свойства введем определение: эксцентриситетом эллипса (гиперболы) называется величина Е, равная E=C/A.
Если обратиться к уравнениям эллипса и гиперболы, то можно получить для Е выражение:
![]() - эллипс
- эллипс
![]() - гипербола
- гипербола
E < 1 для эллипса
E = 0 для окружности
E > 1 для гиперболы
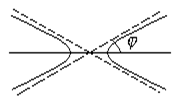 Заметим, что величина эксцентриситета для эллипса характеризует его вытянутость, а для гиперболы – величину угла раствора ветвей гиперболы. Чем больше эксцентриситет гиперболы, тем больше угол раствора ветвей j.
Заметим, что величина эксцентриситета для эллипса характеризует его вытянутость, а для гиперболы – величину угла раствора ветвей гиперболы. Чем больше эксцентриситет гиперболы, тем больше угол раствора ветвей j.
Определение: директрисой D1 эллипса, отвечающей фокусу F1 является прямая, расположенная в той же полуплоскости, что и фокус F1 , перпендикулярно большой оси эллипса на расстоянии ![]() от его центра.
от его центра.
 Уравнение директрисы D1:
Уравнение директрисы D1:
![]()
Уравнение директрисы D2:
![]()
Теперь докажем теорему: отношение расстояния R1 от точки эллипса M(x, y) до фокуса F1 к расстоянию D1 от этой точки эллипса до директрисы D1 есть величина постоянная, равная эксцентриситету эллипса: ![]() .
.
Действительно:
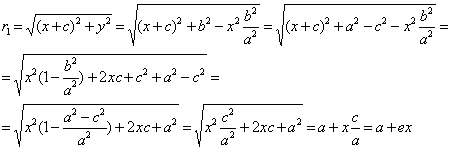 Нормированное уравнение директрисы есть:
Нормированное уравнение директрисы есть:

Расстояние d1, очевидно есть (подставляем координаты точки М в нормированное уравнение):
![]()
Отношение
![]()
![]()
Теорема доказана.
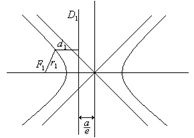 Определим директрису для гиперболы. Директрисой D1 гиперболы, отвечающей фокусу F1 называется прямая, расположенная в полуплоскости, где расположен фокус F1, перпендикулярно действительной оси гиперболы на расстоянии
Определим директрису для гиперболы. Директрисой D1 гиперболы, отвечающей фокусу F1 называется прямая, расположенная в полуплоскости, где расположен фокус F1, перпендикулярно действительной оси гиперболы на расстоянии ![]() от центра.
от центра.
Можно доказать, аналогично эллипсу, теорему: отношение расстояние R1 некоторой точки гиперболы до ее фокуса F1 к расстоянию до директрисы D1 равно ![]() .
.
Эти свойства эллипса и гиперболы позволяют дать новое определение этих кривых. Действительно следующее утверждение: геометрическое место точек М на плоскости, для которых отношение Е расстояния R до точки F к расстоянию D до некоторой прямой D есть величина постоянная, представляет собой эллипс, если E < 1 или параболу, если E = 1, или гиперболу, если е > 1. При этом точка F называется фокусом, а прямая D – директрисой рассматриваемого места точек.
| < Предыдущая | Следующая > |
|---|