31. Нормированное уравнение прямой

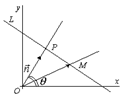
Поставим задачу: выразить уравнение прямой L через два параметра: 1) длину отрезка , где - единичный вектор нормали к прямой 2) угол q между вектором И осью Ох.

Очевидно, .

Точка М(х, у) лежит на прямой L тогда и только тогда, когда проекция на ось, определяемую вектором , равна - длине отрезка , обозначенной за Р.

Если единичный вектор, то в силу определения скалярного произведения, имеем:

Т. е. точка М(х, у) лежит на прямой L тогда и только тогда, когда координаты этой точки удовлетворяют уравнению: .

Это уравнение называется нормированным уравнением прямой.

Как привести уравнение A x + B y + C = 0 к нормированному виду? Так, как уравнения A x + B y + C = 0 и должны определять одну и туже прямую, то должно быть: , или .

Возведем в квадрат и складывая первые два равенства, получим

Знак нужно взять из третьего равенства : поскольку р – расстояние, которое всегда положительно, то знак у t нужно брать противоположным знаку с.

Множитель Взятый со знаком, противоположным знаку слагаемого с, называется нормирующим множителем.

Введем теперь фундаментальное понятие Тклонения произвольной точки М от прямой L. Пусть число d означает расстояние от точки М до прямой L. Назовем отклонением d точки М от прямой L число +d, если точка М и начало координат О лежат по разные стороны от прямой L, и число –d в случае, когда М и О лежат по одну сторону от L.

Если же начало координат лежит на прямой L, то отклонение +d положим, когда М лежит по ту сторону от L, куда направлен нормальный вектор N , и –d в противном случае.

Запишем без доказательства, что левая часть нормированного уравнения прямой равна отклонению точки М с координатами (x, y) от прямой, определяемой этим нормированным уравнением. Это дает возможность легко определить расстояние от точки до прямой. Для этого достаточно нормировать уравнение прямой и подставить в него координаты точки (x, y):

< Предыдущая		Следующая >