30. Угол между двумя прямыми
А). Пусть даны две прямые: A1 x + B1 y + C1 = 0 и A2 x + B2 y + C2 = 0
Т. к. нормальным вектором для первой прямой является вектор ![]() , а для второй
, а для второй ![]() , то задача сводится к определению угла между векторами
, то задача сводится к определению угла между векторами ![]() и
и ![]() . Выполним скалярное произведение двух векторов:
. Выполним скалярное произведение двух векторов: ![]() получим
получим ![]()
Условие параллельности двух прямых, очевидно эквивалентно условию коллинеарности ![]() и
и ![]() :
: ![]()
Условие перпендикулярности – равенство нулю скалярного произведения A1A2 + B1B2=0.
Б). Если две прямые заданы своими каноническими уравнениями
![]() и
и ![]() , то поскольку направляющие векторы этих прямых есть
, то поскольку направляющие векторы этих прямых есть ![]() и
и ![]() , то аналогично предыдущему имеем:
, то аналогично предыдущему имеем:
![]()
Условие паралельности - ![]()
 Условие перпендикулярности - l1l2 = m1m2.
Условие перпендикулярности - l1l2 = m1m2.
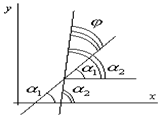
В). Если две прямые L1 и L2 заданы уравнениями с угловыми коэффициентами:
Y = k1 x + b1 и y = k2 x + b2
Из геометрических соображений ясно, что j = a2 - a1
![]()
Условие паралельности - j = 0, tg j = 0, k1 = k2;
Условие перпендикулярности – его можно получить из условия tg j ® ¥, или 1+ k1k2=0, откуда ![]() .
.
| < Предыдущая | Следующая > |
|---|