25. Полярная система координат

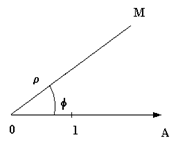
В математике часто применяется эта система. Определяется эта система заданием: некоторой точки 0, называемой Полюсом, луча 0А, исходящего из этой точки, называемого Полярной осью и Масштаба на этой оси.

Полярными координатами точки М Называются два числа: r = ОМ – расстояние от точки М до полюса и j - полярный угол. Угол, отсчитываемый против часовой стрелки, считается положительным. Он определен с точностью до оборота: 2pn. Точку М с полярными координатами r и j обозначают символом М(r, j). Для полюса r = 0, а полярный угол не определен. Для того, чтобы между точками плоскости, отличными от полюса и парами чисел (r, j) существовало взаимно однозначное соответствие, считают, что полярные координаты изменяются в следующих границах:

Полярные координаты легко преобразовать в декартовые, если направить ось Х вдоль полярной оси и совместить полюс с началом координат. Очевидно:

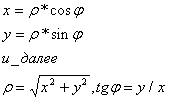
По этим формулам легко переходят от полярных координат к декартовым и наоборот. Так, уравнение окружности радиуса R в полярных координатах есть r=R. Пусть, например, линия в полярной системе координат имеет уравнение%

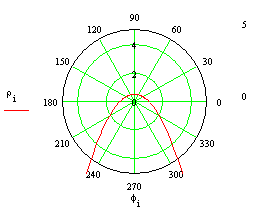
Это парабола

Определение: линия называется алгебраической, если функция Ф(х, у) представляет собой алгебраический полином, т. е сумму конечного числа слагаемых вида

Alk Xl Yk

Можно доказать, что если на плоскости задана произвольная прямая линия, и задана декартова система координат Оху, то прямая L определяется в этой системе координат уравнением первой степени. Иначе Ф(х, у)=Ах+Ву+С полином первой степени. Само доказательство мы опустим.

Докажем теперь, что если на плоскости p фиксирована произвольная система координат Оху, то всякое уравнение первой степени с двумя переменными х, у определяет прямую относительно этой системы.

В самом деле, пусть задано уравнение

Ax + By + C = 0 (**)

Где из А, В, С хотя бы одно не ноль.

Уравнение (**) заведомо имеет хотя бы одно решение х0 у0 (вспомним теорему Кронеккера-Капелли) или:

Ax0 + By0 + C=0 (***)

Вычитая из (**) уравнение (***), получим уравнение

A (x - x0) + B (y - y0)=0

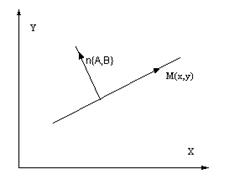
Докажем, что это уравнение определяет прямую L, проходящую через точку х0,у0 и перпендикулярную вектору .

В самом деле, если точка М( х, у ) лежит на L, то ее координаты удовлетворяют уравнению (***), ибо в этом случае векторы и ММ0 = ортогональны и их скалярное произведение

А(х - х0) + В(у - у0)

Равно нулю. Если же точка М( х, у ) не лежит на указанной прямой, то векторы и ММ0 не ортогональны и их скалярное произведение не равно нулю.

Уравнение

Ax + By + C = 0

Называется общим уравнением прямой. Вектор

Называется нормальным вектором прямой (**).

< Предыдущая		Следующая >