08. Ранг матрицы

Запишем определение. Минором K-того порядка матрицы А называется определитель K-того порядка с элементами, лежащими на пересечении любых K строк и любых K Столбцов.

Предположим, что хотя бы один элемент матрицы А отличен от 0. Тогда найдётся такое целое положительное число r, что будут выполнены два условия:

1) у матрицы А имеется минор r-того порядка, отличный от 0;

2) всякий минор (r+1)-го порядка и более (если такие есть), равен нулю.

Число r, удовлетворяющее двум требованиям, назовём Рангом матрицы. А минор R-того порядка, который отличен от нуля, назовём базисным минором. Строки и столбцы, из которых состоит базисный минор, называются базисными строками и базисными столбцами.

Теорема о базисном миноре (без доказательства).

Базисные строки (или столбцы) линейно независимы. Любая строка (столбец) матрицы А является линейной комбинацией базисных строк (столбцов).

Итак, если у матрицы все миноры порядка k>r равны нулю, а среди миноров r-того порядка хотя бы один не равен нулю, то число r называется Рангом матрицы.

Для того, чтобы вычислить ранг матрицы, необходимо, очевидно, вычислить все её миноры и среди них найти минор наибольшего порядка, не равный нулю. Отсюда, кстати следует, что ранг невырожденной матрицы равен порядку матрицы.

Существует, однако, более простое правило вычисления ранга матрицы. Прежде чем к нему обратиться, условимся считать элементарными следующие преобразования матрицы:

1) умножение всех элементов строки на число ;

2) сложение элементов одной строки с элементами другой строки, умноженными на некоторое число ;

3) перемена местами строк матрицы.

Теорема без доказательства: элементарные преобразования матрицы не меняют её ранга.

Поясним всё сказанное простым примером:

Дана матрица А: (*)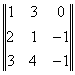

Если посчитать её определитель, то можем убедиться, что она вырождена, её det=0.

Проделаем над ней элементарные преобразования: умножим первую строку на 2 и вычтем из второй, результат запишем во вторую строку; умножим первую строку на три, вычтем из третьей строки и результат запишем в третью строку:

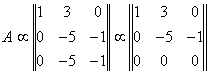
Мы получили матрицу. Раскрывая определитель такой матрицы последовательно сначала по первому столбцу, затем по второму и т. д., легко убедиться, что её определитель равен произведению членов, стоящих на главной диагонали. Отсюда сразу видно, что есть миноры не равные нулю второго порядка: , т. е. ранг такой матрицы равен 2!

В дальнейших лекциях мы будем рассматривать теорию решения систем линейных уравнений, где понятие ранга матрицы имеет решающее значение.

Сейчас обратим своё внимание на пример (*), где квадратная матрица была преобразована в . Этот приём лежит в основе метода решения систем линейных уравнений, называемого методом Гаусса. Вы уже знаете два метода: метод Крамера и метод с использованием обратной матрицы. Они требуют громоздких вычислений определителей. Для практических решений более удобным является способ Гаусса (или способ исключения неизвестных).

Имеем систему:

Матрица этой системы

Исключим из этой системы х1. Для этого умножим каждую строку на ( i = 2,3,…,n) и сложим с первой строкой:

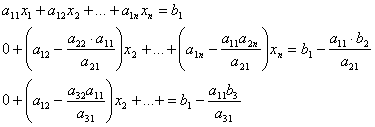
Или 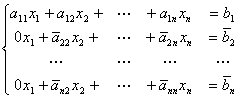далее, умножаем строки i = 3,…,n на и т. д. Придём в итоге к системе:

Отсюда , из предпоследней строки находим значение для :

И т. д.

Первое преобразование называют прямым ходом, второе - обратным. Мы не будем останавливаться здесь на особенностях, которые могут встретиться в решении. Это тема будущих лекций. Пример:

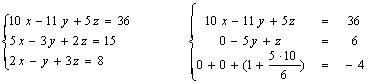
< Предыдущая		Следующая >