22. Дискретная модель накопления и роста

Пусть мы имеем фазовое пространство состояний эволюционирующей системы, для которой определены основные социально-экономические параметры (ВРП, Накопления, Ресурсы и т. п.), выраженные в определенных единицах измерения. Пусть также в этом пространстве могут существовать Элементарные производители, объединяющиеся между собой внутренними и внешними связями. Под словом «существовать» будем понимать «иметь определенные ресурсные параметры». Наличие внутренней связи между элементарными производителями будет указывать на их объединение в одну Подсистему, а наличие внешних связей будет характеризовать взаимодействие подсистем между собой.

Для элементарной подсистемы количество внешних связей ограничено и возникает стремление к расширению, то есть к увеличению числа связей, путем их объединения в подсистему. Процесс «накопления» параметров в фазовом пространстве будет означать переход всей системы с условно выбранного начального (нулевого) состояния на новый уровень с увеличенными параметрами. Если параметры меняются дискретно, то совокупность большого числа переходов (за относительно большой промежуток времени) приведет фазовое пространство, в котором зафиксированы все этапы эволюции, к разбиению на отдельные, в общем случае, не элементарные замкнутые области (вершины графа).

Общие границы между отдельными подсистемами в разбиении выделяют «соседей» выбранной подсистемы, другими словами, количество внешних связей (ребер графа). Таким образом, результат развития системы, будет геометрически представлять собой своеобразную «карту местности» (рис.9), на которую наложен «растущий» из начальной области граф.

 

 

 

 

 

 

 

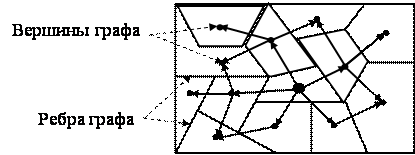Рис. 9. Дерево эволюции системы

Тем не менее, развитие системы, происходящее без разрыва связей должно выглядеть как переход от первого «окружения» исходной области ко второму окружению и т. д. с соблюдением принципа сохранения локальных (индивидуальных) правил соседства. Исследование разбиений показало, что хаотически распределенные локальные связи между подсистемами не приводят к устойчивой динамике роста, пока в качестве согласования на связи не будет наложено условие симметрии. Учитывая важность периодических процессов в природе, выберем в качестве симметрического преобразования элементарные трансляции, образующие решетку. Для конечного числа подсистем это приводит к понятию фундаментальной области периодического разбиения, состоящего из ограниченного набора этих подсистем, трансляционно размноженных (перенесенных) в основных направлениях изменения параметров системы.

Далее, выберем для определенности, в целях удобства представления, в качестве элементарного состояния квадратную ячейку. Тогда подсистемы будут представлять собой объединения клеток с общими сторонами (из двух клеток – домино, из трех – тримино, из большого числа клеток - полимино). Пространство возможных состояний системы, как мы уже определили раньше, будет представлено разбиением плоскости на полимино (рис. 10).

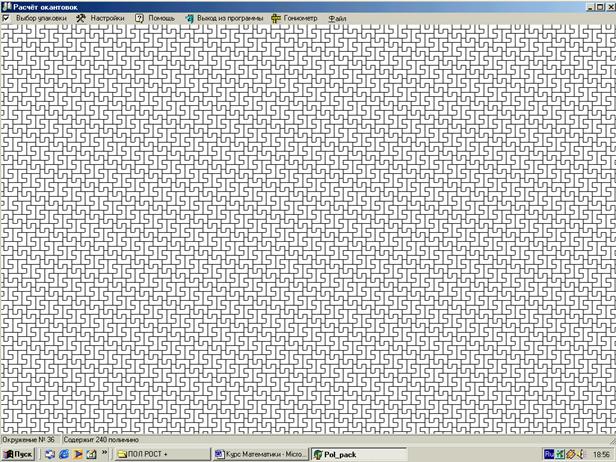
Рис. 10. Разбиение фазового пространства системы на подсистемы (пентамино)

Процесс эволюции системы начинается с выбора исходной подсистемы, ее первого окружения ближайшими соседями, затем второго окружения и так далее, пока не начинает выявляться стационарная структура роста ( Рис.11).

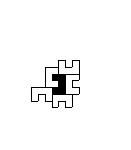
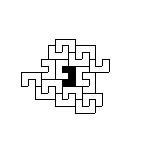
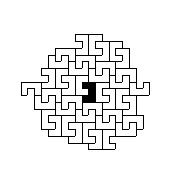
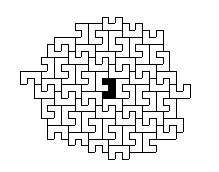
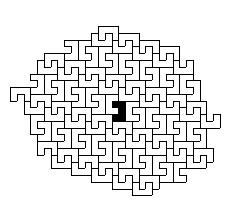
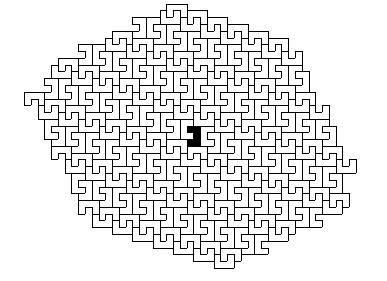
Рис. 11. Поэтапное развитие системы (1 - 5). Стационарная структура (6)

На рис. 12 выделены два «ожерелья» в более сложной системе из 14 полимино – подсистем, которые показывают определенные стадии развития системы, демонстрирующие эффект самоподобия в процессе накопления параметров.

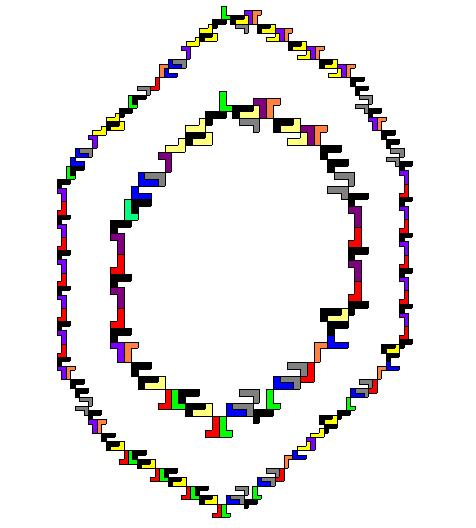
Рис. 12. Два самосогласованных этапа развития системы

Если внутри фундаментальной области взаимодействующих подсистем убирать связывающие полимино границы, то это равносильно объединению их в одну подсистему. В этом случае ход эволюционного развития системы меняется. Легко доказывается, что объединение всех подсистем в фундаментальной области в монопольную единую систему (в двумерной, плоской модели) приводит только к двум возможным вариантам развития: шести - и четырехугольнику. Это однозначно указывает на отсутствие разнообразия при росте монопольных систем. В таких жестких системах сложно что-либо изменить, даже в том случае, когда появляется такая необходимость.

Если далее сравнить гетероструктуры (разнообразные структуры) с монополистическими, то при ухудшении условий, таких как сырьевые ограничения, перебои с энергоресурсами и другими видами ресурсов, монопольная система нарушает стационарный процесс накопления значительно быстрее.

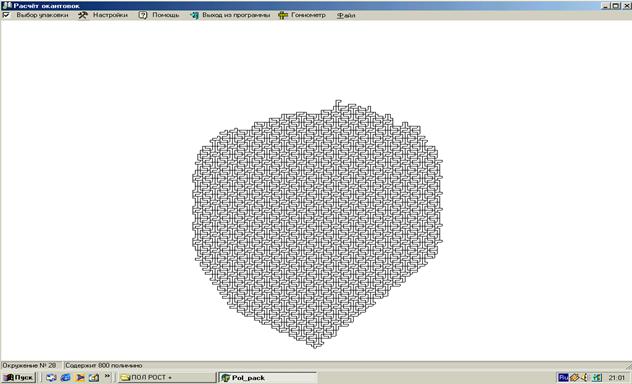
Рис. 13.Ресурсы для гетероструктуры уменьшились «сверху» до 30%

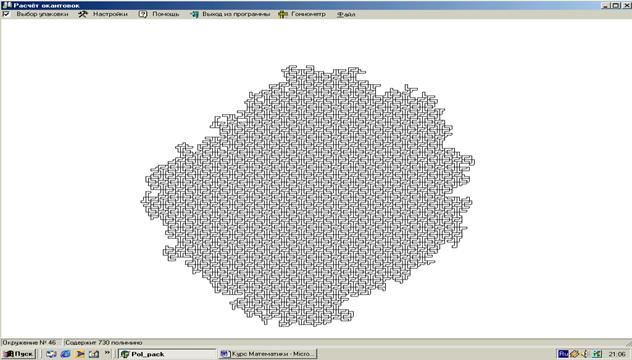
Рис. 14. Ресурсы для гетероструктуры уменьшились со всех сторон до 30%

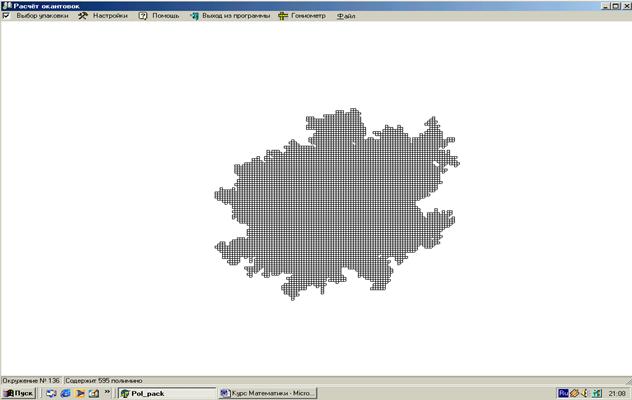
Рис. 15. Ресурсы уменьшились до 45% в монопольной системе

Так как за основу представления дискретного фазового пространства выбрано разбиение на клетки – квадраты, то управление параметрами состояния следует производить либо «сверху» («снизу»), либо «слева» («справа»). При этом, под термином Управление в модели следует понимать задание вероятностей присоединения подсистем сверху, снизу, слева или справа. Если подсистема (полимино) не получает необходимого ресурса, она и не может выйти на последующий уровень развития (присоединиться к последующему уровню), то есть попасть на следующее «ожерелье» (рис. 12). Тогда нарушается согласование роста по направлениям, связанным с соответствующими управляемыми ресурсными параметрами. Рассмотрим этот процесс на конкретных примерах.

На рис. 13, в системе с разнообразными структурами, уменьшение ресурсов до 30% (сверху) привело к нарушению закона развития системы в этом направлении (сравните с пунктирными линиями, характеризующими идеальный рост). Всестороннее ограничение (рис. 14) привело к продолжению роста системы в явно нестационарном режиме.

В монопольной системе (рис. 15) хаотическое развитие происходит в гораздо более выгодных условиях – при 45% - м уменьшении ресурсов, а при ухудшении условий до 40 % Рост вообще прекращается (!). Таким образом, чрезмерная монополизация социально-экономической системы не только не способствует нормальным рыночным отношениям, но и нарушает законы устойчивого развития.

< Предыдущая