19. Математическое моделирование. Математическая модель размножения бактерий

Запишем уравнение, которое было получено при анализе процесса размножения клеток в питательной среде: (III.1) , для решения которого воспользуемся методом разделения переменных:

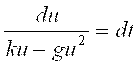, откуда поиск функции U(T) производится интегрированием: . Решение для левой части уравнения можно записать, используя математические таблицы неопределенных интегралов. Сравнивая табличное выражение (13) в Приложении I с последним уравнением, замечаем, что при A = – G ; B = K; C = 0; U = X они совпадают и Δ = 4Ac – B2 = – B2 = – K2, то есть Δ < 0. Поэтому интегрирование левой и правой части приводит к равенству:

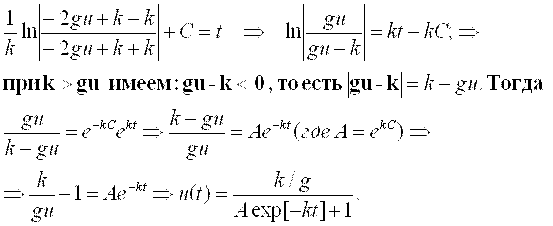
Условие K > Gu является оправданным потому, что в начальный момент времени (t = 0, u = u0 = 1(одна клетка)) скорость роста должна быть положительной величиной. Иначе процесса роста наблюдаться не будет.

Проведем анализ полученного решения : .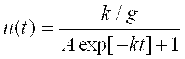

При T→ 0, Exp[-Kt] → 1, а U(T) → Const = U0. С течением времени знаменатель дроби в решении U(T) засчет экспоненциальной функции уменьшается и количество клеток растет. Если на начальной стадии величина Aexp[-Kt] >>1, то рост клеток «идет» почти по экспоненциальному закону, а затем, при T → ∞ величина Aexp[-Kt] становится близкой к нулю и количество клеток «выходит» на стационарную фазу роста: U(T) → K/G.

 

 

 

 

 

 

 

 

 

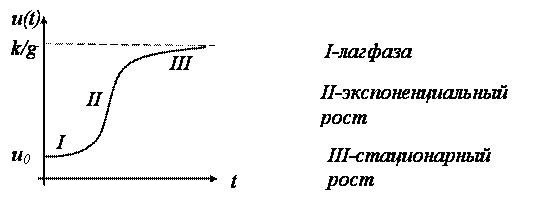Рис. 6. Диаграмма роста

На рис.6 изображена диаграмма роста бактерий в питательной среде, соответствующая особенностям функции U(T). Большая часть ростовых процессов, рассматриваемая в экспериментальной биологии и демографии, имеет аналогичный вид и на диаграмме анализируемого процесса обычно выделяются: фаза накопительная (I), называемая лаг – фазой, (II) – фаза размножения (экспоненциального роста) и (III) – стационарная фаза. Переход от фазы экспоненциального роста к стационарной фазе обычно ассоциируют с моментом возникновения «экологических» проблем, связанных с накоплением в среде продуктов отхода от деятельности организмов. Исследование уравнения роста при произвольных значениях коэффициентов K и G Математическими методами приводит к дискретному аналогу дифференциального уравнения III.1. Если состояние системы фиксируется Не непрерывно, а в определенный момент времени (T = 1, 2 и т. д.), то уравнение для каждой переменной U(T) переходит в уравнение с переменной UT, которое относительно легко решается численными методами. Так, например, рост популяции какого-либо биологического вида с численностью U(T), фиксируемой по годам (T Равно 1 году), может быть описан так называемым логистическим уравнением: UT+1 = CuT (1 – UT), в котором первое слагаемое CuT характеризует рост популяции, а второе –CuT2 (нелинейный член) – определяет ее убыль (см. §8, ЧастьI). Как показал анализ решения, многое зависит от параметра C: однозначность или неоднозначность поведения системы при различных условиях при наличии небольших флуктуаций параметров.

При C < 1 популяция вымирает, при 1 < C < 3 численность растет, при 3 < C < 3,4 наблюдается две ветви (бифуркация), между которыми происходят колебания численности, при 3,4 < C < 3,54 имеется 4 ветви и т. д. и численность начинает "скакать" между ними. При C > 3,57 движение приобретает хаотичный характер (детерминированный хаос). Состояния "перемешиваются" (рис. 7).

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 7. Этапы развития системы

В более сложных системах на каждом переходном этапе точки бифуркаций становятся точками ветвлений и диаграмма процесса принимает вид дерева графа – особой математической структуры, характеризующей множество точек с заданным отношением связи между ними, называемыми ребрами графа. Рис. 7 является частным случаем такой математической структуры. Примерами графов являются алгоритмы разветвленных программ, нейронные сети, транспортные сети, денежные потоки в экономике и многое другое. Последние годы особый интерес почти во всех науках, где используются математические модели эволюционных процессов или процессов роста, привлекают так называемые «растущие» ориентированные (направленные) графы. Применение такого моделирования рассмотрим ниже в последнем примере 4 Приложения III.

< Предыдущая		Следующая >