12. Приложение I
I. Операции с показательными функциями:

II. Операции с логарифмическими функциями:

III. Свойства пределов и операции с пределами:
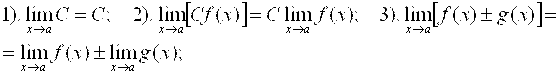
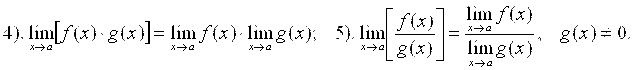
IV. Таблица производных:
1). У = С, у’= 0; 2). У = х, у’ = 1; 3). У = F(X) + G(X), Y’ = F ’ + G ’ ;
4). Y = F(X)G(X), Y’ = F ’G + F G ’; 5) Y = Cf(X), Y’ = Cf ’;
6).  ; 7).
; 7).![]() ;
; 

Дифференцирование сложной функции производится следующим образом:
Для Y = F[U(X)] производная Y’= F’(U)U’(X).
\ V. Свойства неопределенных интегралов:
(1). ![]()
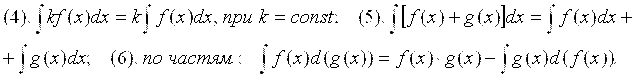
Таблица неопределенных интегралов:

VI. Операции над матрицами.
1. Умножение матрицы на число: В = λА ↔ (Bij = λAij ). Стрелка↔ означает переход от операций, записанных для матриц к соответствующим операциям с матричными элементами (и обратно).
2. Сложение матриц: С = А + В ↔ (Cij = Aij + Bij) . Матрицы должны иметь одинаковый размер.
3. Вычитание матриц: C = A – B = A + (–1)B.
4. Умножение матриц. Эта операция определена только тогда, когда число столбцов (K) первой матрицы А(M×K) равно числу строк (K) второй матрицы В(K×N). Образующаяся при произведении матрица С, имеет m – строк и n – столбцов, то есть ее можно записать: C(M×N).
С = А×В = АВ ↔ Cij = Ai1B1J + Ai2B2J + …+ Aikbkj (I = 1,2,..,M; J = 1,2,..,N).
При умножении матриц произведение АВ не всегда равно произведению ВА. Если можно записать: АВ = ВА, то матрицы А и В – коммутативны (перестановочны), если АВ ≠ ВА, то матрицы некоммутативны.
5. Транспонирование матрицы: Эта операция означает замену строк матрицы на столбцы, тогда каждому элементу Aij исходной матрицы соответствует элемент Aji в транспонированной матрице.
Транспонированная матрица обозначается А’ или АТ.
6. Если в исходной квадратной (M×M) –матрице вычеркнуть одну строку и один столбец, то оставшиеся элементы образуют новую матрицу, «дополнительную» к элементу матрицы, лежащему на пересечении вычеркнутой строки и столбца. Для этой новой матрицы можно продолжить процедуру вычеркивания, пока матрица не окажется простейшей, состоящей из двух строк и столбцов:
М =  .
.
Число Δ = |A| = A11A22 – A12A21 называется Определителем матрицы второго порядка. Можно умножить определитель на элемент Aij из матрицы более высокого (третьего) порядка, к которому матрица была дополнительной и получить новое число, которое называется Минором Mij элемента Aij, а минор, взятый со знаком (–1)i+j называется алгебраическим дополнением Aij этого элемента.
Aij = (–1)i+j Mij.
Тогда для любой квадратной матрицы можно вычислить определитель, используя теорему Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.
Δ = ai1Ai1 + ai2Ai2 + …+ ainAin .
Для того, чтобы при записи отличить матрицу от определителя этой матрицы, определитель часто записывается как модуль величины вертикальными линиями:
 .
.
| < Предыдущая | Следующая > |
|---|