10. Понятие о межотраслевом балансе. Уравнение Леонтьева.

Рассмотрим применение матричного исчисления к задачам в экономической сфере. Для простоты ограничимся анализом взаимодействия двух предприятий, принадлежащих различным отраслям производства товаров. Совокупный продукт, производимый каждым предприятием, можно разделить на три части, одна из которых идет на собственные нужды (πIi), вторая – на обмен с предприятиями другой отрасли производства (πIj) и, наконец, третья часть (Yi) представляет собой объем продукции, идущей к потребителю. Каждая из этих частей имеет денежное выражение, поэтому все величины можно будет сравнивать без какого-либо переводного коэффициента. Система, состоящая из двух предприятий (также можно говорить и о двух отраслях) представлена на схеме (рис.25). Обозначая совокупный продукт первого предприятия X1А второго предприятия X2,

Получаем систему уравнений, верхнее из которых относится первому, а нижнее ко второму предприятию: 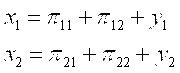. На собственные нужды затрачивается доля А11 от совокупного продукта X1, равная π11/X1, то есть можно записать равенство: А11 = π11/X1. Соответственно, А12 = π12/X2, так как полученный вторым предприятием от первого предприятия поток промежуточного продукта π12 составит долю от совокупного продукта X2 Второго предприятия.

Аналогично рассуждая, имеем: А22 = π22/X2 А21 = π21/X1. Поэтому систему уравнений можно переписать следующим образом:

. (32)

 

 

 

 

 

Рис.25. К межотраслевому балансу двух предприятий

Полученная система уравнений (32), представляющая собой баланс предприятий, может быть записана в матричной форме:

. (33)

Вектор X в этом уравнении представляет собой валовой продукт, вектор Y конечный продукт совместной деятельности предприятий, а матрица А является матрицей прямых затрат. Если в системе совместного выпуска продукции участвует много предприятий и целые отрасли, то векторы становятся многомерными, а матрица затрат имеет высокий порядок. Матричная модель межотраслевого баланса была впервые предложена в экономике нобелевским лауреатом В. Леонтьевым и уравнение (33) называется Уравнением Леонтьева. Рассмотрим различные варианты решений уравнения Леонтьева.

Пример 1. Допустим, что необходимо определить конечный продукт деятельности предприятий (или диктуемое спросом, предложение на рынке) Расчет производится при заданных условиями затратах и знании совокупного продукта предприятий, участвующих в совместной деятельности. Тогда, как это делается с обычными уравнениями, переносится в одну сторону «неизвестное», а в другую – «известное». Из уравнения (33) в этом случае получим матричное уравнение:

Y = X – AX, (34)

которое необходимо решить.

Для решения введем Единичную матрицу I, то есть такую, произведение которой на любую матрицу A не меняет ее коэффициентов Aij. Поэтому такая матрица и названа единичной, поскольку она, так же как обычная единица среди чисел, при умножении не меняет соответствующей величины. По определению единичной матрицы, можно записать, в частности, для матрицы Х следующее выражение: X = I·X. Легко показать, что свойствами единичной матрицы обладает «диагональная» матрица, у которой все элементы с одинаковыми индексами (I = J) равны единице, а с различными индексами (I ≠ J) равны нулю. Действительно, , то есть . Тогда уравнение (34) можно записать следующим образом:

Y = IX –A X = (I – A) X. (35)

В скобках уравнения (35) разность матриц, как и сумма матриц, также является матрицей, которую обозначим В. Тогда и после вычисления соответствующих коэффициентов по известной матрице А, можем найти матрицу Y( по правилу умножения матриц): Y = BX.

Пример 2. Теперь, зная спрос Y и затраты А, найдем совокупный продукт Х. Если бы мы имели дело с числами, то для поиска числа Х, достаточно бы было поделить число Y на число В. Запишем эту процедуру: Х = Y/В = В-1 Y. Умножим слева и справа на В. Тогда ВХ =ВВ-1Y = Y. Для того, чтобы получить аналогичный результат с матрицами, необходима уверенность в том, что существует такая матрица В-1, умножение которой на матрицу В даст единичную матрицу, то есть I = ВВ-1. Матрица В-1 в этом случае имеет право называться обратной матрицей по отношению к матрице В. Итак, если произведение матриц дает единичную матрицу, то они являются Обратными по отношению друг к другу. Процедуру поиска квадратной обратной матрицы произвольного N – го порядка (без доказательства) запишем в виде формулы:

. (36)

В формуле (36) элементами Bij Обратной матрицы являются алгебраические дополнения (31) элементов матрицы В; Det(B) является определителем матрицы В. Символ Т, стоящий на месте показателя степени, обозначает перестановку местами строк и столбцов в матрице, составленной из алгебраических дополнений элементов матрицы В. Такая матрица с элементами Bji называется Транспонированной и обозначается ВТ.

Окончательно имеем: X = B-1Y = (I – A)-1Y.

 

(?): Каким образом из уравнения Леонтьева можно

вычислить матрицу затрат А, зная величину совокупного

и конечного продуктов?

Таким образом, применение матричного исчисления, помимо интегрального и дифференциального, является еще одним примером математического моделирования в социально – экономической сфере жизни людей.

< Предыдущая		Следующая >