15. Лекции 19-20. Нормальные системы дифференциальных уравнений

Система дифференциальных уравнений – это система уравнений относительно независимой переменной x, функций этой переменной и их производных . Система может быть записана в Общем виде

()=0

....................................................................

()=0

Порядок этой системы равен .

Пользуясь теоремой о неявной функции, можно разрешить систему уравнений относительно старших производных и записать ее в Каноническом виде:

()

..................................................................................

()

Теорема. Любое дифференциальное уравнение, разрешенное относительно старшей производной, можно свести к системе дифференциальных уравнений первого порядка.

Доказательство. Рассмотрим дифференциальное уравнение n-ого порядка

. Обозначим . Дифференциальное уравнение n-ого порядка удалось свести к системе n дифференциальных уравнений первого порядка

Применяя эту теорему, можно от канонического вида системы дифференциальных уравнений перейти к системе дифференциальных уравнений первого порядка - Нормальному виду системы.

................

.........................................................................................

.................

Получена система из Дифференциальных уравнений первого порядка.

Удобнее Нормальную систему дифференциальных уравнений (систему в нормальной форме) записывать в виде:

.................................. (Покоординатная форма)

Или в виде

, где 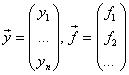(Векторная форма).

Пример. 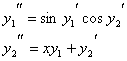Эти уравнения сводятся к нормальной системе

()

()

Оказывается, не только дифференциальное уравнение n- ого порядка сводится к системе n дифференциальных уравнений первого порядка – нормальной системе, но и нормальная система может быть сведена к одному дифференциальному уравнению.

Теорема. Пусть задана система n дифференциальных уравнений первого порядка

..................................

Обозначим

...................................

Потребуем, чтобы функция была бы дифференцируемой по совокупности переменных. Потребуем, чтобы определитель

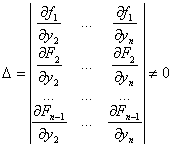
Тогда система n дифференциальных уравнений эквивалентна одному дифференциальному уравнению n-ого порядка.

Доказательство. Метод доказательства называется Методом исключения переменных и применяется на практике при сведении системы к одному уравнению. Продифференцируем :

1) Построим алгоритм метода исключения.

Пусть - решения системы (), тогда уравнения системы Представляют собой тождества

...................................

Получены выражения производных

,

,

,

...

.

Из этих уравнений можно выразить через , так как определитель системы этих уравнений

Подставим выражения через в последнее уравнение . Так как - решения системы , то они являются и решениями полученного уравнения. Следовательно, система сведена к одному уравнению n-ого порядка.

2) Покажем эквивалентность решений. Предположим, что - решения полученного уравнения, покажем, что - решения системы.

, . Обозначим . . Обозначим , и т. д. . Обозначим .

Приравниваем полученные здесь функцииВведенным ранее, сокращая первые и вторые слагаемые, получаем систему уравнений

.....................................

.

Определитель этой системы равен , следовательно, в качестве единственного решения системы имеем . Поэтому решения эквивалентны. Теорема доказана.

Пример.

,

Функция называется Общим решением Системы, если

1) для любого - решение системы

2) для произвольных начальных условий найдется , что .

Если зафиксировать в общем решении, получим Частное решение системы.

Задача Коши.

Найти решение системы , удовлетворяющее заданным начальным условиям .

Теорема Коши о существовании и единственности решения задачи Коши

Пусть функция Непрерывна по совокупности переменных. Пусть существуют и непрерывны частные производные

Тогда существует и единственно решение задачи Коши.

Первые интегралы.

Пусть выполнены условия теоремы Коши. Рассмотрим решение задачи Коши при заданных начальных условиях . По теореме Коши оно существует и единственно. Это решение Можно представить себе как некоторую интегральную кривую, соединяющие точки , .

Если в качестве начальных условий выбрать , то по теореме Коши через эту точку проходит та же единственная интегральная кривая, ее уравнение можно записать в виде . Зафиксируем , обозначим , получим соотношение – Общий Интеграл Системы дифференциальных уравнений (векторное соотношение). Первый интеграл Системы дифференциальных уравнений – скалярная составляющая общего интеграла. Общий Интеграл Системы дифференциальных уравнений – векторная функция, сохраняющая свое значение на решениях системы. Первый интеграл Системы дифференциальных уравнений – скалярная функция, сохраняющая свое значение на решениях системы.

Знание одного первого интеграла позволяет понизить порядок системы на единицу. Знание общего интеграла дает общее решение системы, если только можно разрешить уравнение относительно .

Производной скалярной функции в силу системы называется

.

Скалярная функция является первым интегралом, если

.

Симметричная форма записи системы.

Запишем уравнения системы в нормальной (покоординатной) форме

................................

И запишем эти уравнения в симметричном виде

.

Или, заменяя переменные и правые части ,

Получим Симметричную форму записи системы

.

На переходе к симметричной форме записи основан Метод интегрируемых комбинаций, которым иногда удается получить один или несколько первых интегралов и понизить тем самым порядок системы или решить ее.

Пример.

,

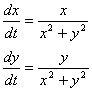Автономные системы и свойства их решений.

Система называется Автономной, если в ее правую часть не входит явно независимая переменная: .

Решение автономной системы можно рассматривать в пространстве координат , которое принято называть Фазовым пространством. Проекция интегральной кривой на это пространство называется Фазовой траекторией (или просто траекторией). Вообще говоря, любую систему можно сделать автономной, вводя дополнительную фазовую координату – независимую переменную и дополнительное уравнение . Фазовое пространство такой системы принято называть Расширенным фазовым пространством.

Свойства решений автономных систем.

1) Если - решение системы, то и тоже решение.

.

Следствие. Фазовая траектория - это та же фазовая траектория, что и .

В самом деле, любая точка первой фазовой траектории является точкой второй фазовой траектории и наоборот.

2) Две фазовых траектории либо не имеют общих точек, либо совпадают.

Пусть две различных фазовых траектории имеют общую точку . Рассмотрим решение .

. Следовательно, по теореме Коши . Но - это траектория , сдвинутая на по аргументу. По следствию, обе фазовые траектории являются одной фазовой траекторией.

Следствие. Множество фазовых траекторий автономной системы в фазовом пространстве представляет собой совокупность непересекающихся кривых.

Точка называется Точкой покоя (точкой равновесия) автономной системы, если .

3) Если точка - точка покоя, то - решение системы.

В самом деле, .

4) Любая фазовая траектория автономной системы есть траектория одного из трех типов:

- Гладкая, не самопересекающаяся кривая,

- Замкнутая гладкая кривая,

- Точка покоя.

Фазовый поток.

Рассмотрим решение задачи Коши автономной системы . Определим Фазовый поток как оператор Сдвига (по аргументу ) по фазовым траекториям системы =.

Рассмотрим некоторую область фазового пространства (фазовым) объемом . Фазовый поток переводит эту область в область объемом .

Справедлива теорема Лиувилля .

Здесь мерой в фазовом пространстве может служить фазовый объем , (дивергенция векторного поля правых частей системы или след матрицы Якоби). Левая часть этой формулы представляет собой изменение фазового объема в единицу «времени» – аргумента, т. е. известный из теории поля поток векторного поля правых частей системы – фазовых скоростей. Приведенная формула аналогична формуле Остроградского – Гаусса в теории поля.

Если , то .

Если , то , что дает формулу для определения фазового объема 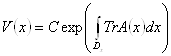, что совпадает с формулой Остроградского – Лиувилля определителя Вронского для линейных автономных систем. Поэтому определитель Вронского имеет смысл фазового объема (определитель всегда имеет смысл некоторого объема, вспомним хотя бы смысл смешанного произведения векторов).

< Предыдущая		Следующая >