13. Лекции 15–16. Линейные дифференциальные уравнения n–ого порядка с переменными коэффициентами

Линейное Однородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

Линейное Неоднородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

Если коэффициенты и правая часть – непрерывные функции и , то условия теоремы Коши выполнены, Решения однородного и неоднородного уравнений существуют и единственны.

Введем линейный дифференциальный оператор

Здесь Обозначает оператор дифференцирования .

Тогда Линейное однородное уравнение можно записать в виде , а Линейное неоднородное – в виде .

Так как линеен, то

Пользуясь линейностью оператора, легко доказать Теоремы о свойствах решений однородного и неоднородного уравнений (ниже обозначено - решение однородного уравнения, - решение неоднородного уравнения).

Теоремы о свойствах решений.

1) Сумма или разность решений однородного уравнения есть решение однородного уравнения,

2) Разность решений неоднородного уравнения есть решение однородного уравнения,

3) Сумма решений однородного и неоднородного уравнений есть решение неоднородного уравнения.

Докажем эти теоремы.

3) .

Теорема. Решения линейного однородного уравнения с переменными коэффициентами образуют линейное пространство.

Доказательство. Так как сумма любых двух решений однородного уравнения и произведение любого решения на число вновь есть решения однородного уравнения, то операции сложения и умножения на число на множестве решений определены корректно (не выводят за множество решений).

Решения образуют аддитивную группу по сложению (абелев модуль). В самом деле, ассоциативность по сложению очевидна, (тривиальное решение) является решением однородного уравнения, для каждого решения противоположное решение тоже является решением. Следовательно, решения однородного уравнения – группа по сложению. Аддитивность решений очевидна, поэтому эта группа аддитивна. Справедливость четырех аксиом из восьми показана. Существует число «1», такое что - решение, справедлива ассоциативность по умножению на число . Это – две аксиомы относительно операции умножения на число. Наконец, справедливы две аксиомы дистрибутивности, связывающие операции сложения и умножения на число .

Итак, налицо полный набор из восьми аксиом. Продумайте их еще раз подробнее дома.

Линейная зависимость и независимость.

Функции называются Линейно независимыми, если

(допустима только тривиальная линейная комбинация функций, тождественно равная нулю). В отличие от линейной независимости векторов здесь тождество линейной комбинации нулю, а не равенство. Это и понятно, так как равенство линейной комбинации нулю должно быть выполнено при любом значении аргумента.

Функции называются Линейно зависимыми, если существует не нулевой набор констант (не все константы равны нулю) , такой что (существует нетривиальная линейная комбинация функций, тождественно равная нулю).

Теорема. Для того чтобы функции были линейно зависимы, необходимо и достаточно, чтобы какая-либо из них линейно выражалась через остальные (представлялась в виде их линейной комбинации).

Докажите эту теорему самостоятельно, она доказывается так же, как аналогичная ей теорема о линейной зависимости векторов.

Определитель Вронского.

Определитель Вронского для функций вводится как определитель, столбцами которого являются производные этих функций от нулевого (сами функции) до n-1 го порядка.

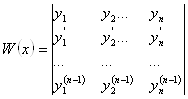Теорема. Если функции линейно зависимы, то

Доказательство. Так как функции линейно зависимы, то какая-либо из них линейно выражается через остальные, например,

. Тождество можно дифференцировать, поэтому

. Тогда первый столбец определителя Вронского линейно выражается через остальные столбцы, поэтому определитель Вронского тождественно равен нулю.

Теорема. Для того, чтобы решения линейного однородного дифференциального уравнения N-ого порядка были линейно зависимы, необходимо и достаточно, чтобы .

Доказательство. Необходимость следует из предыдущей теоремы.

Достаточность. Зафиксируем некоторую точку . Так как , то столбцы определителя, вычисленные в этой точке, представляют собой линейно зависимые векторы.

, что выполнены соотношения

Так как линейная комбинация решений линейного однородного уравнения является его решением, то можно ввести решение вида

- линейную комбинацию решений с теми же коэффициентами.

Заметим, что при это решение удовлетворяет нулевым начальным условиям, это следует из выписанной выше системы уравнений. Но тривиальное решение линейного однородного уравнения тоже удовлетворяет тем же нулевым начальным условиям. Поэтому из теоремы Коши следует, что введенное решение тождественно равно тривиальному, следовательно,

Поэтому решения линейно зависимы.

Следствие. Если определитель Вронского, построенный на решениях линейного однородного уравнения, обращается в нуль хотя бы в одной точке, то он тождественно равен нулю.

Доказательство. Если , то решения линейно зависимы, следовательно, .

Теорема. 1. Для линейной зависимости решений необходимо и достаточно (или ).

2. Для линейной независимости решений необходимо и достаточно .

Доказательство. Первое утверждение следует из доказанной выше теоремы и следствия. Второе утверждение легко доказывается от противного.

Пусть решения линейно независимы. Если , то решения линейно зависимы. Противоречие. Следовательно, .

Пусть . Если решения линейно зависимы, то , Следовательно, , противоречие. Поэтому решения линейно независимы.

Следствие. Обращение определителя Вронского в нуль хотя бы в одной точке является критерием линейной зависимости решений линейного однородного уравнения.

Отличие определителя Вронского от нуля является критерием линейной независимости решений линейного однородного уравнения.

Теорема. Размерность пространства решений линейного однородного уравнения N-ого порядка равна N.

Доказательство.

1. Покажем, что существуют n линейно независимых решений линейного однородного дифференциального уравнения n-го порядка. Рассмотрим решения , удовлетворяющие следующим начальным условиям:

...........................................................

Такие решения существуют. В самом деле, по теореме Коши через точку проходит единственная интегральная кривая – решение. Через точку проходит решение , через точку

- решение , через точку - решение .

Эти решения линейно независимы, так как .

2. Покажем, что любое решение линейного однородного уравнения линейно выражается через эти решения (является их линейной комбинацией).

Рассмотрим два решения. Одно - произвольное решение с начальными условиями . Справедливо соотношение

..........................................................................

, где

Второе решение – это линейная комбинация решений с теми же коэффициентами .

Вычисляя начальные условия в точке для решения , убеждаемся, что они совпадают с начальными условиями для решения . Следовательно, по теореме Коши, произвольное решение представляется в виде линейной комбинации линейно независимых решений .

Таким, образом, существует n линейно независимых решений линейного однородного дифференциального уравнения n-ого порядка, и произвольное решение линейно выражается через эти решения. Поэтому размерность пространства решений линейного однородного дифференциального уравнения n-ого порядка равна n. .

Любые n линейно независимых решений линейного однородного дифференциального уравнения n-ого порядка представляют собой Базис Пространства решений или Фундаментальную систему решений.

Теорема о структуре общего решения однородного уравнения.

Общее решение линейного однородного уравнения есть линейная комбинация решений фундаментальной системы.

Доказательство. Покажем, что линейная комбинация

является общим решениям (удовлетворяет пунктам определения общего решения)

1. - решение линейного однородного уравнения как линейная комбинация решений.

2. Зададим произвольные начальные условия , покажем, что можно подобрать константы такие, что удовлетворяет этим начальным условиям.

.........................................................................

Это – система линейных алгебраических уравнений относительно констант . Определитель этой системы – определитель Вронского. Он не равен нулю, так как решения линейно независимы. Поэтому константы определяются из этой системы по начальным условиям – правым частям системы единственным образом.

Следовательно, - общее решение.

Замечание. Определитель Вронского (как всякий определитель) представляет собой ориентированный n – мерный объем, натянутый на векторы решений фундаментальной системы решений.

Формула Остроградского – Лиувилля.

Рассмотрим линейное однородное уравнение

Определитель Вронского можно вычислить по Формуле Остроградского – Лиувилля

Вывод формулы Остроградского – Лиувилля.

Известна формула для производной определителя

Вычислим ...+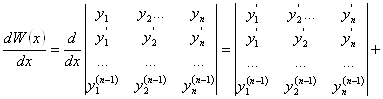

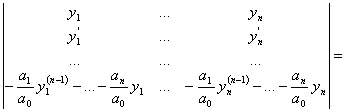
0+...+0+ .

, .

Замечание. В формуле Остроградского – Лиувилля участвуют только коэффициенты при двух старших производных.

Рассмотрим частный случай уравнения второго порядка.

. Здесь формулу Остроградского – Лиувилля можно вывести проще. Рассмотрим - два частных решения

. , . Умножим первое уравнение на , а второе на и вычтем первое уравнение из второго.

Так как , то = .

Теперь уравнение можно переписать в виде . Решая это уравнение с разделяющимися переменными, получаем формулу Остроградского – Лиувилля

Формула для построения второго частного решения по известному

(построение фундаментальной системы).

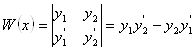
Разделим обе части уравнения на

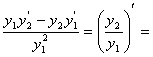
Отсюда . Нам надо найти частное решение, поэтому выберем С=1, C 1=0, получим .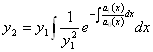

Теорема о структуре общего решения неоднородного уравнения.

Общее решение линейного неоднородного уравнения есть сумма частного решения линейного неоднородного уравнения и общего решения однородного уравнения.

Доказательство. Покажем, что - общее решение неоднородного уравнения.

1. - решение неоднородного уравнения как сумма решений однородного и неоднородного уравнений (теоремы о свойствах решений).

2. Зададим произвольные начальные условия , . Вычислим начальные условия для выбранного частного решения неоднородного уравнения . Получим систему линейных алгебраических уравнений для определения констант:

.........................................................................

Определитель этой системы – определитель Вронского. Он не равен нулю, так как решения линейно независимы. Поэтому константы определяются из этой системы по начальным условиям – правым частям системы единственным образом. Следовательно, - общее решение неоднородного уравнения.

Метод вариации произвольной постоянной Для линейного неоднородного дифференциального уравнения n-ого порядка. . ().

Здесь обозначено , заметим, если - решение однородного уравнения, то .

Заметим, всегда, применяя метод вариации, надо делить на коэффициент при старшей производной, т. е. приводить уравнение.

Пусть найдено решение однородного уравнения

Варьируем произвольные постоянные, ищем решение неоднородного уравнения в виде

Дифференцируем это соотношение

Потребуем, чтобы

Тогда .

Дифференцируем еще раз

Потребуем, чтобы

Тогда .

Вновь дифференцируем и т. д., в результате, после n-2 дифференцирования получим

Дифференцируем и подставляем

В неоднородное уравнение .

Так как - решения однородного уравнения, то .

Получим .

Это – последнее уравнение системы для определения варьированных констант. Соберем все уравнения в Систему для определения констант.

........................................................

Так как определитель системы – определитель Вронского, не равный нулю в силу линейной независимости решений, то функции Определяются из этой системы однозначно.

Теперь общее решение неоднородного уравнения определяется по формуле .

< Предыдущая		Следующая >