11. Лекция 13. Геометрическая интерпретация дифференциальных уравнений 1 порядка, изоклины. Особые точки и особые решения
Рассмотрим интегральные кривые дифференциального уравнения 1 порядка ![]() . В любой точке плоскости OXY правая часть дифференциального уравнения известна, ее можно вычислить. Поэтому в любой точке плоскости известна и левая часть. Левая часть, исходя из геометрического смысла производной, задает тангенс угла наклона касательной к интегральной кривой.
. В любой точке плоскости OXY правая часть дифференциального уравнения известна, ее можно вычислить. Поэтому в любой точке плоскости известна и левая часть. Левая часть, исходя из геометрического смысла производной, задает тангенс угла наклона касательной к интегральной кривой.
Следовательно, в любой точке плоскости можно определить угол наклона (к оси OX) касательной к интегральной кривой, проходящей через эту точку, т. е. определить Направление вектора касательной к интегральной кривоЙ.
Если в некоторой области плоскости задана вектор-функция, то говорят, что она задает в этой области Векторное поле.
Поэтому геометрический смысл дифференциального уравнения первого порядка состоит в том, что оно задает в области определения G (x, y) функции f(x, y) векторное поле Направлений векторов касательных к интегральным кривым. Если интерпретировать дифференциальное уравнение механически, как скорость f(x, y) движения точки по траектории – интегральной кривой, то дифференциальное уравнение задает Поле скоростей.
Изоклинами Называются кривые в плоскости OXY, в каждой точке которой угол ![]() наклона к оси OX касательной к интегральной кривой один и тот же
наклона к оси OX касательной к интегральной кривой один и тот же ![]() . Уравнение изоклины:
. Уравнение изоклины: ![]() .
.
Строя изоклины как можно чаще, можно достаточно точно построить интегральные кривые, нанося на каждой изоклине соответствующее ей направление вектора касательной к интегральной кривой..
Пример. ![]()
Уравнение изоклины ![]()
|
|
|
Уравнение изоклины |
|
0 |
0 |
x=0 (ось OY) |
|
1 |
|
y = - x |
|
-1 |
|
y = x |
|
|
|
y = 0 (ось OX) |
Можно предположить, что уравнение интегральной кривой ![]() (это легко проверить:
(это легко проверить: ![]() ).
).
Таким образом, интегральные кривые – окружности с центром в начале координат.
Понятие об особых точках и особых решениях дифференциального уравнения первого порядка.
Точка (x, y) называется Не особой точкой дифференциального уравнения первого порядка ![]() , если существует ее окрестность, что через каждую точку этой окрестности проходит единственная интегральная кривая.
, если существует ее окрестность, что через каждую точку этой окрестности проходит единственная интегральная кривая.
Все прочие точки называются Особыми точками Дифференциального уравнения первого порядка ![]() .
.
Особым решением называется решение, все точки (x, y) которого – особые.
Пример. ![]()
Решая это уравнение с разделяющимися переменными, получим общее решение ![]() и решение, не принадлежащее этому семейству – тривиальное решение
и решение, не принадлежащее этому семейству – тривиальное решение ![]() .
.
Каждая точка оси OX – особая, так как через нее проходят как тривиальное решение, так и частное решение из семейства ![]() .
.
![]() - особое решение.
- особое решение.
Пример. ![]()
Заметим, что ![]() . Общее решение
. Общее решение ![]() (иначе
(иначе ![]() ). Кроме того,
). Кроме того, ![]() - тоже решение.
- тоже решение. ![]() - особое решение.
- особое решение.
Заметим, что на особом решении не выполняются условия теоремы Коши, гарантирующие единственность. В самом деле, в том и другом примерах ![]() терпят разрыв при
терпят разрыв при ![]() .
.
Уравнения первого порядка, не разрешенные относительно производной.
Рассмотрим два типа уравнений 1) ![]() .
.
Метод введения параметра.
Обозначим ![]()
В случае 1) ![]() ,
, 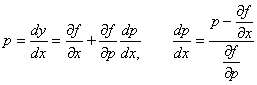 .
.
Найдем решение ![]() , подставим в
, подставим в ![]() ,
,
Получим ![]() - общее решение.
- общее решение.
В случае 2) 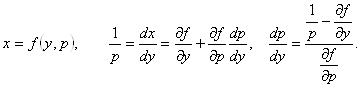
Найдем решение ![]() , подставим в
, подставим в ![]() ,
,
Получим ![]() - общее решение.
- общее решение.
Уравнение Лагранжа. ![]()
Дифференцируем:
![]() ,
, ![]()
![]() - линейное уравнение.
- линейное уравнение.
Отыскиваем ![]() И, подставляя в уравнение Лагранжа, находим
И, подставляя в уравнение Лагранжа, находим ![]() .
.
Пример. ![]()
![]() - уравнение Лагранжа.
- уравнение Лагранжа.
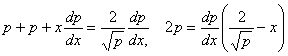 ,
,
![]() - линейное уравнение по
- линейное уравнение по ![]() .
.
Решаем его методом подстановки
 .
.
Уравнение Клеро. ![]() .
.
Уравнение Лагранжа превращается в уравнение Клеро, если в уравнении Лагранжа положить ![]() .
.
Дифференцируем обе части:
![]() .
.
1) ![]() - общее решение.
- общее решение.
2) ![]() . Подставляя в уравнение, получим особое решение
. Подставляя в уравнение, получим особое решение ![]()
Пример. ![]()
![]()
1) ![]() - общее решение
- общее решение
2) 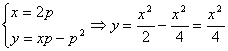 - особое решение.
- особое решение.
| < Предыдущая | Следующая > |
|---|