10. Лекция 12. Основные типы дифференциальных уравнений первого порядка

Уравнения с разделяющимися переменными.

Уравнение с разделяющимися переменными имеет вид

В этом уравнении переменные «можно разделить», т. е. функции от x и dx собрать в правую часть, а функции от y и dy – в левую часть. Затем интегрируем полученное соотношение и получаем соотношение вида .

Пример. . Заметим, что - решение, это так называемое тривиальное решение. Только, проанализировав, является ли решением или нет, мы имеем право, разделив обе части на , двигаться дальше. Иначе тривиальное решение будет потеряно.

Здесь нельзя потерять модуль, иначе потеряем решения при .

Обозначим и раскроем модуль:

Заменим И разрешим С быть равной нулю, т. к. тривиальное решение есть. Окончательно,

, где С – произвольная действительная постоянная.

Обычно все эти «подводные камни» опускают (достаточно сказать о них один раз) и сразу выписывают решение уравнения .

Пример. Найти кривую, проходящую через точку , если угловой коэффициент касательной к кривой в три раза больше углового коэффициента радиус-вектора в точке касания.

- решение, . Подставляя начальные условия, получим .

Пример. Формула Циолковского.

Ракета вместе с топливом, массой , движется прямолинейно, без учета гравитации. Скорость истечения топлива , в начальный момент времени ракета неподвижна и имеет вместе с топливом массу M. Вывести формулы для скорости ракеты .

Выделим элемент массы dm. По закону сохранения количества движения

Подставляя , получим . Отсюда

- формула Циолковского.

Однородное уравнение.

Правая часть однородного уравнения зависит от отношения :

Это позволяет заменить отношение новой переменной или .

Получено уравнение с разделяющимися переменными. Если , то исходное уравнение уже является уравнением с разделяющимися переменными.

Пример. . , ,

Обобщенно-однородное уравнение.

Обобщенно-однородное уравнение имеет вид

Возможны два случая

1) Рекомендуется замена ,

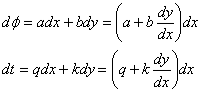
, получили однородное уравнение.

Здесь вводят новую функцию старой переменной x.

, где Определяются из пропорциональности строк определителя. Получено уравнение с разделяющимися переменными.

Пример. , случай1).

, ,

Получили однородное уравнение.

Пример. , случай 2).

Получили уравнение с разделяющимися переменными.

Линейное уравнение.

Существует два метода решения линейного уравнения: метод вариации произвольной постоянной и метод подстановки.

Метод вариации произвольной постоянной будет встречаться нам часто: при решении неоднородных линейных уравнений высшего порядка, при решении неоднородных систем линейных уравнений. Его надо знать твердо.

При решении Методом вариации произвольной постоянной сначала решают однородное уравнение (с нулевой правой частью)

Это – уравнение с разделяющимися переменными.

Затем варьируют произвольную постоянную, полагая .

Подставляем в неоднородное уравнение:

При вариации произвольной постоянной здесь обязательно должны сократиться два члена, в этом идея метода.

, где С – произвольная постоянная.

Видно, что общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Это справедливо не только для линейных уравнений первого порядка, но и для линейных уравнений высших порядков, и для линейных систем. Там подобное утверждение называется теоремой о структуре общего решения неоднородного уравнения или системы.

Замечание. Решая уравнение методом вариации, Обязательно приводите его к виду (если при Стоит коэффициент, то делить на него обязательно), иначе метод вариации даст ошибку.

При решении Методом подстановки полагают

. Мы видели выше, что решение действительно является произведением двух функций от x. Этот факт здесь и используется.

. Подставляем в уравнение:

Теперь решают либо уравнение , определяя отсюда

, либо уравнение , определяя отсюда

. Здесь при интегрировании не надо добавлять константу, она появится позже, при отыскании второй функции. В первом случае, остается найти v из .

Теперь =, как и выше.

Во втором случае остается найти u из , .

Теперь =, как и выше.

Пример. .

Решение методом вариации. Приводим уравнение, деля на коэффициент при :

Решаем однородное уравнение .

Варьируем произвольную постоянную .

Подставляем в неоднородное уравнение

Решение методом подстановки.

Уравнение Бернулли.

Если n = 1, то это – уравнение с разделяющимися переменными, если n = 0, то это – линейное уравнение.

Заметим, что при n > 0 - решение уравнения.

Решать уравнение Бернулли можно тремя способами

1) Сведение к линейному уравнению заменой

Разделим обе части уравнения на ,

Получили линейное уравнение относительно .

Этот метод применяется редко, так как уравнение Бернулли можно решать теми же методами, что и линейное уравнение, не приводя его предварительно к линейному.

2) Решение методом вариации произвольной постоянной.

Решение проводится аналогично линейному уравнению.

Решим сначала однородное уравнение, полагая правую часть уравнения нулевой.

Затем Ищем решение уравнения в виде , варьируя произвольную постоянную ,

Вычисляем и подставляем в исходное уравнение.

Вновь, как и в линейном уравнении, два слагаемых сокращаются, получаем уравнение с разделяющимися переменными.

Определяя отсюда функцию , подставляем ее в .

3)Решение методом подстановки.

Полагаем , подставляем в исходное уравнение

Точно так же, как при решении линейного уравнения, решаем, например, уравнение . Подставляем полученную функцию, решаем «оставшееся» уравнение с разделяющимися переменными .

Заметим, что оно получилось точно таким же, как в методе вариации. Поэтому вторая функция в методе подстановки и есть та самая варьируемая постоянная. Затем записываем решение .

Видим, что метод вариации и метод подстановки, фактически, один и тот же метод. Просто в методе подстановки с самого начала используется то, что решение представляется в виде произведения двух функций независимой переменной.

Пример.

Решим это уравнение Бернулли методом вариации произвольной постоянной.

Уравнение в полных дифференциалах.

Любое дифференциальное уравнение первого порядка, разрешенное относительно старшей производной, можно записать в виде

Если выполнено соотношение , то уравнение называется Уравнением в полных дифференциалах.

Причину такого названия понять легко. Пусть - функция двух переменных, дифференцируемая и имеющая непрерывные вторые частные производные по своим переменным. Тогда .

Если обозначить , то исходное уравнение можно записать в виде полного дифференциала

, а соотношение как раз и означает равенство смешанных производных .

Поэтому решить уравнение в полных дифференциалах – означает найти функцию (она называется потенциалом). Так как на решениях дифференциального уравнения, то потенциал будет первым интегралом исходного дифференциального уравнения:

Для решения уравнения в полных дифференциалах можно использовать два способа.

1) ,

Здесь интегрирование ведется «частным образом»: только по переменной x, считая y константой или только по y, считая x константой.

Сравнивая оба выражения для , находим функции и константы.

Если какой-либо из интегралов, например, не берется или его вычислить сложно, то можно найти +.

Затем, дифференцируя частным образом по x, надо сравнить с и определить функции и константы.

2) Потенциал можно определять по формуле (она будет выведена из независимости криволинейного интеграла от пути интегрирования позже, в 3 семестре)

Пример. .

Решим уравнение первым способом.

Так как , то это – уравнение в полных дифференциалах.

Сравнивая оба равенства, видим, что , поэтому . Соотношение - это первый интеграл заданного дифференциального уравнения.

Решим уравнение вторым способом.

. Здесь принято .

Интегрирующий множитель.

Можно поставить вопрос, нельзя ли любое дифференциальное уравнение первого порядка свести к уравнению в полных дифференциалах?

Оказывается, что существует такой Интегрирующий множитель , умножая на который обе части любого дифференциального уравнения, удовлетворяющего условиям теоремы Коши, можно привести это уравнение к уравнению в полных дифференциалах.

Однако неясно, как в общем случае найти этот интегрирующий множитель. Ясно только, что он должен удовлетворять уравнению

Оказывается, если (является функций только одной переменной x), то . Если (является функций только одной переменной y), то .

Пример. .

Покажите, что здесь выполняется первое условие и .

Найдите потенциал, покажите, что он равен .

< Предыдущая		Следующая >