2.6.1. Различные виды уравнения прямой. Прямая как пересечение плоскостей
Прямую ![]() можно задать как пересечение двух не парал-лельных плоскостей
можно задать как пересечение двух не парал-лельных плоскостей ![]() и
и ![]()
![]() (1)
(1)
Сразу заметим, что направляющий вектор ![]() прямой
прямой ![]() должен быть перпендикулярен нормальным векторам
должен быть перпендикулярен нормальным векторам ![]() и
и ![]() плоскостей
плоскостей ![]() и
и ![]() , т. е.
, т. е.
 .
.
Отсюда следует, что
![]() .
.
Осталось выбрать точку ![]() через которую проходит искомая прямая
через которую проходит искомая прямая ![]() . Заметим, что если плоскости
. Заметим, что если плоскости ![]() и
и ![]() не параллельны, то хотя бы один из коэффициентов
не параллельны, то хотя бы один из коэффициентов ![]() отличен от нуля. Пусть
отличен от нуля. Пусть ![]() . Тогда возьмем
. Тогда возьмем ![]() произвольным числом, например,
произвольным числом, например, ![]() . Остальные координаты
. Остальные координаты ![]() найдем из системы (1)
найдем из системы (1)
![]() .
.
Таким образом, искомые канонические уравнения прямой имеют вид
![]()
Или
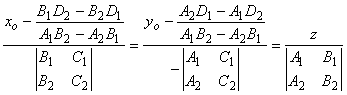 .
.
Пример. Написать канонические уравнения и уравнения в проекциях прямой, заданной общими уравнениями:
![]()
Решение. Найдем направляющий вектор искомой прямой

Найдем точку ![]() через которую проходит искомая прямая. Для этого положим произвольно
через которую проходит искомая прямая. Для этого положим произвольно ![]() , например,
, например, ![]() в исходной системе, получим систему
в исходной системе, получим систему ![]() , ее решение
, ее решение ![]() , а уравнение прямой имеет вид:
, а уравнение прямой имеет вид:
![]()
Приравнивая попарно каждое из равенств (их три), получим уравнения прямой в проекциях на координатные плоскости:
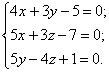
| < Предыдущая | Следующая > |
|---|