7.3. Необходимый признак сходимости числового ряда
Теорема. Для сходимости любого числового ряда (1.1) необходимо, чтобы An ® 0 при N® ∞ , то есть чтобы ![]() .
.
Доказательство. Допустим, что ряд (1.1) сходится. Это значит, что существует и конечна его сумма S∞, которая определяется пределом (1.4). Учитывая, что ![]() , откуда следует, что
, откуда следует, что ![]() , получаем:
, получаем:
![]()
То есть действительно An ® 0 при N ® ∞ . Теорема доказана.
Из доказанной теоремы следует, что Если An не стремится к нулю при N® ∞, то ряд сходиться не может – он заведомо расходится.
Примечание. Условие An ® 0 при N® ∞ является необходимым, но не достаточным условием сходимости числового ряда (1.1). Это значит, что оно еще не гарантирует сходимости ряда. Иначе говоря, возможна ситуация, когда при An ® 0 при N® ∞ , и тем не менее ряд (1.1) расходится.
Классическим примером такого ряда является Гармонический ряд
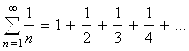 (1.16)
(1.16)
Необходимое условие сходимости ![]() при N® ∞ для этого ряда очевидным образом выполняется. И тем не менее этот ряд расходится, так как его сумма S= ∞ .
при N® ∞ для этого ряда очевидным образом выполняется. И тем не менее этот ряд расходится, так как его сумма S= ∞ .
 Докажем это. Для этого рассмотрим рис. 7.1. На этом рисунке изображена бесконечно протяженная в горизонтальном направлении ступенчатая фигура, состоящая из заштрихованных прямоугольников, площади которых соответственно равны (
Докажем это. Для этого рассмотрим рис. 7.1. На этом рисунке изображена бесконечно протяженная в горизонтальном направлении ступенчатая фигура, состоящая из заштрихованных прямоугольников, площади которых соответственно равны (![]() …). То есть суммарная площадь S этой заштрихованной фигуры как раз равна сумме S гармонического ряда (1.16). Но эта площадь S заведомо больше площади S0 между осью Ох и гиперболой
…). То есть суммарная площадь S этой заштрихованной фигуры как раз равна сумме S гармонического ряда (1.16). Но эта площадь S заведомо больше площади S0 между осью Ох и гиперболой ![]() в пределах для Х от 1 до ¥. А
в пределах для Х от 1 до ¥. А
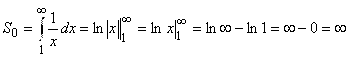 .
.
И так как S > S0 , то и S = ∞. Таким образом, гармонический ряд расходится, ибо его сумма S равна ∞:
![]() (1.17)
(1.17)
| < Предыдущая | Следующая > |
|---|