4.18. Приближенное решение уравнений методом половинного деления
Пусть требуется решить некоторое уравнение ![]() . Решить его – это значит найти все его корни. То есть найти те значения неизвестной X, которые удовлетворят уравнению. Корни уравнения
. Решить его – это значит найти все его корни. То есть найти те значения неизвестной X, которые удовлетворят уравнению. Корни уравнения ![]() имеют и наглядный геометрический смысл: это точки пересечения графика функции
имеют и наглядный геометрический смысл: это точки пересечения графика функции ![]() С осью Ох.
С осью Ох.
Пусть ![]() – непрерывная на заданном отрезке
– непрерывная на заданном отрезке ![]() функция, то есть ее график – сплошная (непрерывная) линия для всех X этого отрезка. Тогда очевидно следующее: если на концах этого отрезка (в точках A и B) функция
функция, то есть ее график – сплошная (непрерывная) линия для всех X этого отрезка. Тогда очевидно следующее: если на концах этого отрезка (в точках A и B) функция ![]() принимает значения разных знаков, то график этой функции непременно пересечет отрезок
принимает значения разных знаков, то график этой функции непременно пересечет отрезок ![]() оси Ох хотя бы один раз. А значит, уравнение
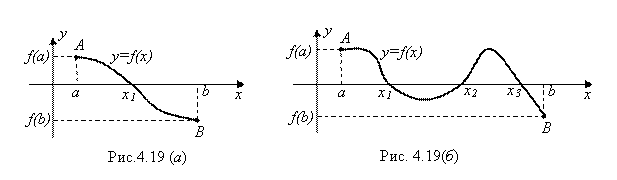
оси Ох хотя бы один раз. А значит, уравнение ![]() заведомо будет иметь на этом отрезке хотя бы один корень (один корень X1 на рис. 4.19 (А) и три корня (X1, X2, X3) на рис. 4.19 (Б)).
заведомо будет иметь на этом отрезке хотя бы один корень (один корень X1 на рис. 4.19 (А) и три корня (X1, X2, X3) на рис. 4.19 (Б)).
В частности, если на отрезке ![]() функция
функция ![]() дифференцируема (это значит, что на отрезке
дифференцируема (это значит, что на отрезке ![]() в каждой его точке X существует производная
в каждой его точке X существует производная ![]() ), и эта производная на всем отрезке сохраняет свой знак, то при знаке (+) этой производной функция
), и эта производная на всем отрезке сохраняет свой знак, то при знаке (+) этой производной функция ![]() на отрезке
на отрезке ![]() монотонно растет, а при знаке (–) монотонно убывает. В любом из этих вариантов график функции
монотонно растет, а при знаке (–) монотонно убывает. В любом из этих вариантов график функции ![]() , имеющей на концах отрезка
, имеющей на концах отрезка ![]() значения разных знаков, пересечет этот отрезок только один раз (как, например, на рис. 4.19 (А)). А значит, уравнение
значения разных знаков, пересечет этот отрезок только один раз (как, например, на рис. 4.19 (А)). А значит, уравнение ![]() будет иметь на отрезке
будет иметь на отрезке ![]() только один корень X1.
только один корень X1.
Простейшим и вместе с тем эффективным методом численного нахождения этого корня X1 является Метод половинного деления. Суть его в следующем:
1) Находим середину С1 отрезка ![]() и вычисляем
и вычисляем ![]() . Искомый корень X1 окажется, очевидно, в той из половин
. Искомый корень X1 окажется, очевидно, в той из половин ![]() или
или ![]() отрезка
отрезка ![]() , на концах которой функция
, на концах которой функция ![]() имеет разные знаки. Выбираем эту половину.
имеет разные знаки. Выбираем эту половину.
2) Находим середину С2 той половины отрезка ![]() , на которой находится искомый корень X1, и вычисляем
, на которой находится искомый корень X1, и вычисляем ![]() . Выбираем ту половину найденной в пункте 1 половины, на концах которой функция
. Выбираем ту половину найденной в пункте 1 половины, на концах которой функция ![]() имеет разные знаки. Именно на ней находится искомый корень X1 уравнения
имеет разные знаки. Именно на ней находится искомый корень X1 уравнения ![]() .
.
3) Потом полученный отрезок (четвертинку исходного отрезка ![]() ) опять делим пополам, и т. д.
) опять делим пополам, и т. д.
В итоге, последовательно сужая промежуток оси Ох, на котором содержится искомый корень X1 уравнения ![]() , через несколько шагов получим достаточно узкий промежуток (например, через 10 шагов исходный промежуток
, через несколько шагов получим достаточно узкий промежуток (например, через 10 шагов исходный промежуток ![]() уменьшится в
уменьшится в ![]() раз, через 20 шагов – в
раз, через 20 шагов – в ![]() миллион раз, и т. д.). Любая точка этого промежутка (например, его середина) может быть принята за приближенное значение искомого корня X1. И корень этот, очевидно, может быть найден с любой заданной точностью, что и делается с помощью соответствующей программы на ЭВМ.
миллион раз, и т. д.). Любая точка этого промежутка (например, его середина) может быть принята за приближенное значение искомого корня X1. И корень этот, очевидно, может быть найден с любой заданной точностью, что и делается с помощью соответствующей программы на ЭВМ.
Примечание. Если известно, что уравнение ![]() имеет несколько корней (X1, X2, …) – см. например, рис. 4.19 (Б), то отделяя каждый из них своим промежутком и используя для каждого такого промежутка изложенную выше схему половинного деления, можно найти все эти корни. А чтобы узнать, сколько корней имеется у данного уравнения
имеет несколько корней (X1, X2, …) – см. например, рис. 4.19 (Б), то отделяя каждый из них своим промежутком и используя для каждого такого промежутка изложенную выше схему половинного деления, можно найти все эти корни. А чтобы узнать, сколько корней имеется у данного уравнения ![]() , следует представлять себе, хотя бы в общих чертах, график функции
, следует представлять себе, хотя бы в общих чертах, график функции ![]() . То есть нужно исследовать эту функцию. И в этом исследовании главное – это определение интервалов непрерывности и точек разрыва функции, исследование ее на четность-нечетность и периодичность, определение интервалов возрастания-убывания и точек экстремума.
. То есть нужно исследовать эту функцию. И в этом исследовании главное – это определение интервалов непрерывности и точек разрыва функции, исследование ее на четность-нечетность и периодичность, определение интервалов возрастания-убывания и точек экстремума.
Пример 1. Определить количество корней уравнения ![]() И отделить некоторым промежутком каждый из них.
И отделить некоторым промежутком каждый из них.
Решение. Рассмотрим функцию ![]() . Эта функция определена (а следовательно, и непрерывна) для всех X,
. Эта функция определена (а следовательно, и непрерывна) для всех X, ![]() . Функция эта общего вида (ни четная и ни нечетная) и не периодическая.
. Функция эта общего вида (ни четная и ни нечетная) и не периодическая.
Далее, исследуя ее на возрастание-убывание и точки экстремума (проделайте это по изложенной выше схеме самостоятельно), устанавливаем, что интервалы ![]() и
и ![]() являются интервалами возрастания функции, а интервал
являются интервалами возрастания функции, а интервал ![]() – интервал ее убывания;
– интервал ее убывания; ![]() – точка максимума функции, а точка
– точка максимума функции, а точка ![]() – вершина ее графика;
– вершина ее графика; ![]() – точка минимума функции, а точка
– точка минимума функции, а точка ![]() – впадина ее графика. При
– впадина ее графика. При ![]() функция
функция ![]() , а при
, а при ![]() функция
функция ![]() . По этим результатам можно уже схематично построить график функции
. По этим результатам можно уже схематично построить график функции ![]() (рис. 4.20). Из этого графика видим, что он пересекает ось Ох три раза – в точках (X1, X2, X3). То есть уравнение
(рис. 4.20). Из этого графика видим, что он пересекает ось Ох три раза – в точках (X1, X2, X3). То есть уравнение ![]() имеет три корня (X1, X2, X3). Корень X1 находится на промежутке
имеет три корня (X1, X2, X3). Корень X1 находится на промежутке ![]() ; корень X2 – на промежутке
; корень X2 – на промежутке ![]() , корень X3 – на промежутке
, корень X3 – на промежутке ![]() . Каждый из них с любой заданной точностью может быть найден изложенным выше методом половинного деления.
. Каждый из них с любой заданной точностью может быть найден изложенным выше методом половинного деления.
Впрочем, так как ![]() – точное значение второго корня, то можно точно найти и значения корней X1 и X3:
– точное значение второго корня, то можно точно найти и значения корней X1 и X3:
![]()
| < Предыдущая | Следующая > |
|---|