2.03. Числовые характеристики выборочной средней и выборочной дисперсии. Оценки числовых характеристик генеральной совокупности

Как отмечено в конце предыдущего параграфа, числовые характеристики выборки ; ; ; являются случайными величинами. В связи с этим возникает естественный и важный для практики вопрос о математическом ожидании, дисперсии и прочих числовых характеристиках этих случайных величин.

Начнём с важнейшей из этих величин – с выборочной средней . Будем считать, что объём N генеральной совокупности настолько велик, что объём N выборки можно считать малой величиной по сравнению с N . Поэтому последовательный отбор из генеральной совокупности каждого отбираемого объекта практически не нарушает состава генеральной совокупности – она как бы всё время остаётся целой.

Обозначим через (Х1; Х2; …Хп) случайные величины, выражающие значения исследуемого признака Х при отборе первого, второго, … N-ого объектов выборки. С учётом предположения, сделанного выше относительно объёма генеральной совокупности, можем считать, что случайные величины (Х1; Х2; …Хn) одинаково распределены и независимы. Распределение каждой из них совпадает с с распределением величины Х1 - с распределением признака Х у первого отобранного объекта. Если (Х1; х2; ... хр) – список всех возможных значений исследуемого признака Х в генеральной совокупности, то случайная величина Х1 имеет возможность принять любое из этих значений. А их вероятности будут, очевидно, равны (), где () – количества объектов генеральной совокупности, имеющих соответственно значения (Х1; х2; ... хр). Таким образом, закон распределения величины Х1, а вместе с нею и остальных случайных величин (Х2; Х3; …Хп), будет иметь вид:

			…		(K=1, 2, …N) (2.1)
			…

Выборочная средняя - это, очевидно, средняя арифметическая из случайных величин (Х1; Х2; …Хn):

= (2.2)

Если объём N Выборки достаточно большой (хотя и много меньше объёма N генеральной совокупности), то согласно (2.2) выборочная средняя является суммой большого числа независимых случайных величин. А потому, согласно теореме Ляпунова (часть Ι, глава 2, §4), можем считать, что случайная величина распределена приблизительно по нормальному закону. Причём это будет При любом законе распределения величин (Х1; Х2; …Хn), то есть При любом законе распределения признака Х в генеральной совокупности. А если есть основания считать, что признак Х в генеральной совокупности распределён нормально (что обычно и имеет место), то распределение случайной величины , как суммы независимых нормально распределённых случайных величин, будет нормальным при любом, в том числе и малом, объёме N выборки.

Действительно, распределения случайных величин (Х1; Х2; …Хn) при очень большом объёме генеральной совокупности можно считать совпадающими с распределением величины Х1. Но если величина Х1 приняла некоторое значение Xi, то это значит, что признак Х принял это значение. То есть распределения Х И Х1, а значит распределения Х и (Х1; Х2; …Хn) совпадают. И все эти величины являются нормальными, если распределение величины Х нормальное. Но тогда и все слагаемые в (2.2) распределены нормально, а вместе с ними, в силу их независимости, и величина распределена нормально.

В общем, так или иначе, мы практически всегда можем считать величину распределённой нормально (мы не можем этого утверждать лишь в случае, когда выборка имеет малый объём N и при этом исследуемый признак Х заведомо не распределён нормально).

Найдём параметры и нормально распределённой случайной величины . Для этого сначала вычислим математическое ожидание и дисперсию случайных величин Хк (K=1, 2,…N). В соответствии с таблицей (2.1) и формулами (1.4) и (1.23) (часть I, глава 2) имеем:

(2.3)

Здесь и – числовые характеристики генеральной совокупности (генеральная средняя и генеральная дисперсия). А тогда на основании (2.2) и свойств математического ожидания и дисперсии (см. часть I, глава 2) получим:

(2.4)

Итак, нормально распределённая случайная величина распределена с параметрами и .

Свои числовые характеристики имеет и выборочная дисперсия . Она уже заведомо не распределена нормально, ибо по природе своей имеет лишь неотрицательные значения. Из ее числовых характеристик приведем лишь важнейшую – математическое ожидание (среднее значение):

(2.5)

Кстати, если объем N выборки достаточно велик, то 1, и тогда можно считать, что

Докажем формулу (2.5). Согласно определения (1.5) выборочной дисперсии, ее можно выразить через введенные выше случайные величины (X,…) формулой:

(2.6)

Тогда

(2.7)

Так как случайные величины (X,…) имеют одинаковые распределения, то все N слагаемых в сумме (2.7) одинаковы, и поэтому

(2.8)

То есть

(2.9)

Найдем каждое из трех слагаемых, входящих в (2.9).

1) Найдем . Так как

= -,

То

= + = (2.10)

2) Найдем :

Так как величины (X,…) независимы, то

=

== (2.11)

3) Найдём Так как

То

(2.12)

Подставляя выражения (2.10), (2.11) и (2.12) в (2.9), мы и получим доказываемое равенство (2.5).

Анализируя формулы (2.4) для выборочной средней , видим, что математическое ожидание (среднее значение) выборочной средней равно средней генеральной . При этом разброс этих значений вокруг будет уменьшаться с увеличением объема N выборки, ибо, согласно (2.4),

При (2.13)

Таким образом, если нам нужно по выборке оценить неизвестную генеральную среднюю , то эта оценка будет такой:

(2.14)

Причем эта оценка будет тем точнее (надежнее), чем больше будет объем N выборки.

Анализируя теперь формулу (2.5), видим, что . То есть возможные значения выборочной дисперсии (значения для разных выборок) группируются не вокруг генеральной дисперсии , а вокруг Несколько меньшего числа То есть является Смещенной оценкой . Для устранения этого смещения введем так называемую Исправленную выборочную дисперсию :

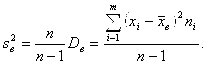
(2.15)

При этом Называется Исправленным выборочным средним квадратическим отклонением. Математическое ожидание (среднее значение) уже равно. Действительно:

(2.16)

Таким образом, исправленная выборочная дисперсия имеет среднее значение, равное генеральной дисперсии и, таким образом, является Несмещенной оценкой для генеральной дисперсии:

(2.17)

Замечание. Исправленная выборочная дисперсия , согласно её выражения (2.15), является суммой квадратов отклонений вариант выборки от их среднего значения , Рассчитанной на одну степень свободы этой суммы.

Действительно, объём выборки равен N, значит и всех вариант в выборке тоже N. Будь в сумме

(2.18)

Все эти варианты независимыми, эта сумма квадратов отклонений вариант от

Выборочной средней имела бы N степеней свободы - по числу независимых вариант , участвующих в формировании этой суммы. Однако эти варианты в сумме (2.18) не являются независимыми, ибо через них по первой из формул (1.5) вычисляется выборочная средняя , фигурирующая в этой сумме. Формула (1.5) представляет собой линейное соотношение

, (2.19)

Cвязывающее варианты . Из него одну из вариант (любую) можно выразить через остальные N-1 вариант. Так что в сумме (2.18) содержится только N-1 независимых слагаемых, в силу чего она имеет не N, а N-1 степеней свободы. Так что исправленная выборочная дисперсия (несмещённая оценка генеральной дисперсии ), согласно (2.15), действительно представляет собой сумму (2.18), рассчитанную на её одну степень свободы. Такое истолкование исправленной выборочной дисперсии (несмещённой оценки дисперсии генеральной) нами ещё позднее не раз будет использоваться.

Исходя из оценок (2.14) и (2.17), можем получить еще две оценки для неизвестных числовых характеристик генеральной совокупности:

(2.20)

Оценки (2.14), (2.17) и (2.20) числовых характеристик ,,, % генеральной совокупности называются Точечными оценками, ибо эти оценки осуществляются одним числом (точкой). Все эти оценки несмещённые, и они тем точнее (надёжнее), чем больше объем N выборки.

Кроме точечных оценок числовых характеристик генеральной совокупности, вводятся также и их Интервальные оценки.

Пусть, например, - некоторая из выборочных числовых характеристик (, или , или , и т. д.), а - соответствующая ей генеральная характеристика. И пусть , так что мы имеем точечную несмещённую оценку . Нас, естественно, интересует точность этой оценки, то есть разность . Но так как по выборочным данным вычисляется лишь , а неизвестна, то разность эту точно найти нельзя. Её можно лишь попытаться оценить. А именно, можно лишь поставить вопрос: с какой вероятностью можно утверждать, что , где - некоторое заданное положительное число? Или, что одно и то же, какова вероятность того, что ?

Интервал Называется Доверительным интервалом для оценки ; число Называется Точностью интервальной оценки ; вероятность называется Надежностью интервальной оценки . Все эти понятия связываются в следующем равенстве:

(2.21)

Геометрическая иллюстрация этого равенства изображена на рис. 3.3. Этот рисунок иллюстрирует смысл равенства (2.21): с вероятностью неизвестная содержится в своем доверительном интервале

Очевидно, чем шире доверительный интервал (то есть чем больше ), тем больше надежность (вероятность) того, что принадлежит этому интервалу. И наоборот, чем ýже доверительный интервал (меньше ), тем меньше вероятность того, что содержится в этом интервале. Заметим, что широкий доверительный интервал означает малую точность оценки величины , а узкий – наоборот, высокую. Таким образом, чем выше точность оценки , тем меньше её надежность, а чем ниже точность – тем больше надежность, что вполне естественно.

Нас, естественно, будет интересовать конкретная математическая связь между шириной доверительного интервала и вероятностью того, что содержится в этом интервале. Очевидно, что наиболее важно ответить на этот вопрос, когда . Этим мы и ограничимся.

Как отмечалось выше, точечной оценкой для является , которая распределена нормально с математическим ожиданием и средним квадратическим отклонением (формулы (2.4)). Заменяя в (2.21) на , на и пользуясь формулой (4.11) (часть I, глава 2) для нормально распределённых случайных величин, получим:

(2.22)

Урожайность (Ц/га)	Площадь (Га)	(2.24)
12-14	18
14-16	57
16-18	109
18-20	136
20-22	83
22-24	66
24-26	31
Итого	500

Таким образом, точность , определяющая ширину доверительного интервала для оценки генеральной средней , и надёжность этой оценки связаны друг с другом равенством:

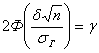, откуда , где 2 (2.23)

Неизвестное среднее квадратическое отклонение генеральной совокупности можно в (2.23) заменить, согласно (2.20), его точечной оценкой . Однако эта замена будет достаточно точной, а значит, и оправданной лишь при достаточно большом объеме N Выборки (скажем, при N>30).

Пример 1. Выборочным путём были получены следующие данные об урожайности ржи в некотором зерновом регионе (таблица 2.24). Найти вероятность того, что средняя урожайность ржи, полученная в выборке, отличается в ту или в другую сторону (то есть по абсолютной величине) от средней урожайности на всей площади региона, занятой под рожь, не более чем на 0,2 ц/га.

Решение. Площадь региона, занятая рожью, нам неизвестна. Но она нам и не нужна. Важно лишь, чтобы она была намного больше тех 500 га, которые попали в выборку, что мы и будем предполагать. В соответствии с условием задачи нам требуется найти вероятность (надёжность) того, что , где - средняя урожайность ржи в выборке, а - средняя урожайность ржи во всем регионе. Эту надежность найдем по формуле (2.23). В ней следует положить , (-велико!), а величину заменим на :

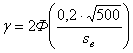(2.25)

Исправленное выборочное среднее квадратическое отклонение найдем из статистического распределения выборки (2.24). Для этого сначала приведем его к дискретному виду:

(урожайность в ц/га)	13	15	17	19	21	23	25	(2.26)
(площадь в га)	18	57	109	136	83	66	31

Применяя затем формулы (1.5), получим:

А тогда, согласно (2.15), получаем:
.

Подставляя найденное значение в (2.25), получим искомую вероятность (надежность) :

Итак, с надежностью (с 86%-ой надежностью) можем утверждать, что средняя урожайность ржи во всем регионе отличается от средней урожайности 19,1 ц/га на обследованных выборочно 500 га по абсолютной величине не более, чем на 0,2 ц/га. Или, что одно и тоже, с 86%-ой надежностью можем утверждать, что находится в следующем доверительном интервале:

18,9 ц/га<<19,3 ц/га.

Если объем выборки небольшой (N<30), то пользоваться формулой (2.23), просто заменив в ней на , не рекомендуется, ибо Может значительно отличаться от , а значит, могут получаться слишком грубые результаты. Но если исследуемый признак Х распределен нормально, то доказано, что при любых, в том числе малых, объемах N выборки случайная величина

(2.27)

Имеет распределение Стьюдента с степенями свободы (см, глава 16, §16). И поскольку плотность вероятности такой случайной величины известна и является четной функцией своего аргумента T (см. часть I, глава 2, §4), то для любого вероятность осуществления неравенства -<T< найдется по формуле (2.28), следующей из формулы (3.6) главы 2, часть I:

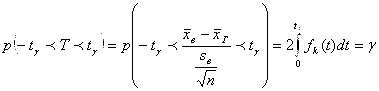(2.28)

Или, что одно и то же:

, где , (2.29)

А величина Связана с и последним равенством (2.28). Составлена специальная таблица (см. таблицу 4 Приложения) – так называемая таблица критических точек распределения Стьюдента, позволяющая по заданным и находить . А значит, в соответствии с (2.29), находить величину , определяющую доверительный интервал (; для оценки генеральной средней с надежностью (вероятностью) . И это – для любых значениях N, в том числе и для малых. При больших же N (N>30) указанный доверительный интервал, найденный посредством вычисления как по формуле (2.23) при замене в ней на , так и по формуле (2.29), оказывается практически одинаковым.

Пример 2. Девять независимых повторных измерений некоторой величины А дали следующие результаты:

1,24; 1,26; 1,25; 1,23; 1,25; 1,24; 1,24; 1,25; 1,24

Оценить с помощью доверительного интервала истинное значение А измеряемой величины с надёжностью (95%-ой надёжностью).

Решение. Будем рассматривать результаты всех девяти повторных измерений величины А как выборочные значения случайной величины Х – результата отдельного измерения этой величины. Тогда статистическое распределение выборки будет иметь вид:

	1,23	1,24	1,25	1,26	(N=1+4+3+1=9) (2.30)
	1	4	3	1

А генеральной совокупностью в данном случае будет, очевидно, бесконечное множество всех возможных значений одного измерения (N= Случайная величина X, как мы знаем (§4, глава 2) распределена нормально. Её параметры A и должны быть приняты за и . При этом А - это искомое значение измеряемой величины.

Так как объём N выборки невелик (N=9), то для интервальной оценки =A Следует использовать равенства (2.29).

Исходя из статистического распределения выборки (2.30), найдём и :

Далее по заданным =0,95 и K =N-1=9-1=8 с помощью таблицы 4 Приложения найдём значение , входящие в выражение (2.29) для : =2,31. Таким образом,

Следовательно, искомый доверительный интервал (; , содержащий с надёжностью =0,95 (с 95%-ой надёжностью) истинное значение А = измеряемой величины, будет таким: (1,234; 1,255).

В заключении этого параграфа рассмотрим следующий важный для практики вопрос: каков минимальный объём N Выборки, обеспечивающий оценку неизвестной генеральной средней с заданной точностью при заданной надёжности ?

Очевидно, что искомое минимальное значение объёма выборки при не слишком широком доверительном интервале (; , то есть при не слишком большом , и при не слишком малой надёжности того, что будет содержаться в это интервале, следует ожидать достаточно большим. И это Будет тем больше, чем меньше будет (точнее оценка) и чем больше будет (надежнее оценка) генеральной средней . Поэтому для нахождения этого значения первоначально следует использовать формулы (2.23), применяемые при N>30, из которых следует:

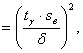где (2.31)

Но если найденное значение Окажется небольшим (<30), то тогда для его уточнения следует использовать последнее равенство (2.29), приводящее, кстати, к тому же выражению для , что и (2.31). Только следует находить не из равенства , то есть не из таблицы интеграла вероятности Ф(Х), а подбирать из таблицы 4 Приложения для критических точек распределения Стьюдента..

Пример 3. Выборочным путем исследуется зерно, связанное с убранного поля на элеватор. Требуется определить минимальный объём выборки, проводимой с целью определения средней массы одного зерна, чтобы с вероятностью 0,99 ошибка в определении этой средней массы не превысила по абсолютной величине 0,002 г. По данным предыдущих выборок установлено, что 0,014г.

Решение. По таблице функции Ф(Х) (по таблице 2 Приложения) из равенства =0.99 находим :

Теперь по формуле (2.31) находим искомый минимальный объём выборки:

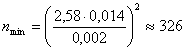
Упражнения

1. С целью исследования размера X некоторых однотипных изделий, выпускаемых заводом, было случайным образом отобрано 50 изделий. Их распределение по размеру (статистическое распределение выборки) имеет вид:

X (см)	107,8- -108,0	108,0- -108,2	108,2- -108,4	108,4- -108,6	108,6- -108,8	108,8- -109,0
N	1	4	16	18	8	3

Найти доверительный интервал, оценивающий с надёжностью средний размер изделий, выпускаемых заводом.

Ответ: (108,39; 108,51).

2. При определении экспериментальным путём значения некоторой величины А проведено 5 повторных опытов, которые дали следующие результаты:

0,640; 0,652; 0,656; 0,664; 0,670.

А) Какова вероятность того, что истинное значение А Измеряемой величины отличается от среднего результата проведённых измерений не более, чем на 0,01?

Б) В каком доверительном интервале (; с надёжностью =0,99 находится искомое значение А?

Ответ: а) 0,87; б) (0,633; 0,680)

3. Проверку качества большой партии изделий проводят выборочным путём. Каков должен быть минимальный объём выборки, чтобы с надёжностью =0,99 можно было утверждать, что отклонение среднего срока службы изделия в выборке отличается от среднего срока службы во всей исследуемой партии не более, чем на 3 часа (в ту или в другую сторону)? По результатам предварительной (пробной) выборки получено 10 час.

Ответ: 74.

< Предыдущая		Следующая >