2.02. Генеральная совокупность и выборка

Пусть имеется большая совокупность однотипных объектов (зёрен в ворохе зерна, деревьев в лесу, жителей в стране, предметов массового производства, и т. д.), подлежащая изучению. При этом предметом изучения являются какие-то качественные или количественные параметры объектов, составляющих данную совокупность (скажем, пригодность объектов к использованию, их вес, сорт, размер, и т. д.), законы распределения этих параметров и многое другое (об этом конкретнее будет сказано позже).

Исходная совокупность объектов называется Генеральной совокупностью, а число N объектов этой совокупности (обычно очень большое и точно не известное) называется Объёмом генеральной совокупности.

Произвести сплошное обследование (обследование всех объектов) генеральной совокупности, в силу её огромного объёма, не представляется возможным. А если это обследование связано с порчей или даже уничтожением обследуемых объектов (скажем, нас интересует сила, при действии которой объект ломается), то оно и бессмысленно (исследовать все объекты генеральной совокупности – это значит все их переломать). Поэтому изучают только небольшую, случайно отобранную, часть этой совокупности (горсть зёрен из вороха, небольшую часть деревьев леса, случайно отобранных жителей страны, небольшую партию предметов массового производства, и т. д.).

Отобранная совокупность объектов называется Выборочной совокупностью или, короче, Выборкой. Количество N Объектов, попавших в выборку, называется Объёмом выборки. Как правило, объём N Выборки много меньше объёма N генеральной совокупности (N « N ). Объекты выборки подвергаются сплошному обследованию, а затем, по результатам этого обследования, делаются определенные выводы и обо всей генеральной совокупности.

Естественно, что обследование объектов выборки не даст полной и точной информации о всей генеральной совокупности (ведь обследуется лишь часть объектов этой совокупности). Поэтому любые выводы, касающиеся генеральной совокупности, к которым мы придем на основании исследования выборки, чреваты неточностями и даже ошибками. Но эти ошибки, естественно, будут тем менее вероятны и тем меньше по величине, чем больше будет N – Объем выборки. Как именно от объема выборки зависит точность и надежность получаемых выводов о генеральной совокупности – эти вопросы тоже рассматриваются в математической статистике.

Кроме большого объема, для получения достаточно надежных и достоверных выводов о генеральной совокупности выборка должна еще адекватно представлять собой генеральную совокупность. Или, как ещё говорят, она должна быть Репрезентативной. Это значит, что нельзя отбирать преимущественно лучшие или, наоборот, худшие объекты. Правильным (репрезентативным) будет такой отбор, при котором шансы быть отобранными у всех объектов генеральной совокупности будут одинаковыми. А это будет иметь место лишь в том случае, когда выборку объектов из генеральной совокупности осуществляют Случайно.

Например, чтобы отбор гости зерна из вороха зерна был произведён репрезентативно, следует взять по щепотке зёрен из разных мест этого вороха (с разных краёв, с поверхности, с глубины, и т. д.). А если этот ворох лежит давно и уже слежался (однородность вороха нарушилась), то перед осуществлением выборки ворох этот хорошо бы и тщательно перемешать.

В тех случаях, когда объекты генеральной совокупности пронумерованы (например, это автомобили, выпускаемые автозаводом, или отдельные части этих автомобилей – моторы, кузова, и т. д.), для случайного отбора каких-то N объектов такой генеральной совокупности можно воспользоваться так называемой Таблицей случайных чисел. То есть номера отбираемых объектов можно взять из этой таблицы, открыв страницу таблицы наугад. Эту таблицу получают с помощью ЭВМ, и она содержится во многих справочниках по математической статистике. Кстати, числа, содержащиеся в таблице случайных чисел – это просто наборы цифр дробной части случайной величины X, равномерно распределённой на отрезке [0;1].

После того, как выборка произведена, исследуют Каждый объект этой выборки. То есть выясняют (измеряют, устанавливают) значения тех количественных или качественных признаков отобранных объектов, которые представляют исследовательский интерес в генеральной совокупности. Например, если исследуется выборочным путём ворох зерна, то качественным признаком каждого отобранного зерна может быть годность его к посеву или к использованию в мукомольной промышленности. А количественным признаком – вес зерна, количественно выраженная влажность, процентное содержание белка, клейковины и т. д. Другой пример: если генеральная совокупность представляет собой некоторые изделия массового производства, то качественным признаком каждого отобранного изделия может быть его стандартность, а количественным – контролируемый размер изделия, или его вес, или время до выхода его из строя, и т. д.

Будем пока считать, что у объектов генеральной совокупности исследуется лишь один признак Х, и этот признак – Количественный (то есть его можно выразить некоторым числом). Это может быть вес, сорт, размер, и т. д. Кстати, при необходимости и качественный признак объектов (например, их годность к своему назначению) можно сделать количественным, если считать, что этот признак Х=1, если объект годен, и считать Х=0, если объект не годен.

Итак, пусть из изучаемой генеральной совокупности сделана случайная выборка объёмом N. И пусть оказалось, что у N1 объектов, попавших в выборку, значение исследуемого признака Х оказалось равным Х1, у N2 Объектов – значение Х2, …, у Nm объектов – значение Хm. Тогда таблица

			…		(1.1)
			…

Содержащая указанные данные, называется Статистическим распределением выборки. При этом числа (Х1; х2;. . . хm), представляющие собой все встретившиеся в выборке значения исследуемого признака Х, называются Вариантами, а количества (N1; n2;. . . nm) объектов, имеющих соответствующие варианты, называются Частотами.

Статистическое распределение выборки автоматически имеет вид (1.1), если исследуемый признак Х является дискретной (прерывистой) величиной. Например, если исследуется экзаменационная оценка по какому-либо предмету большого количества студентов, то эта оценка Х по своей природе является величиной дискретной (принимает лишь значения 2; 3; 4; 5). И если выборка составляет, например, 25 человек, то её статистическое распределение может быть, например, следующим:

	2	3	4	5	(2+8+10+5=25) (1.2)
	2	8	10	5

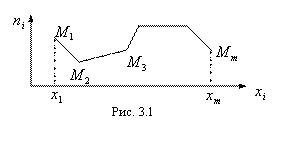Статистическое распределение выборки (1.1) для наглядности изображают графически – в виде так называемого Полигона частот, представляющего собой ломаную линию с узлами в точках - см. рис.3.1.

Если же исследуемый признак Х Является непрерывной величиной, то статистическое распределение выборки обычно оформляют в виде таблицы (1.3.):

	-	-	…	-	(1.3)
			…

Здесь (Х1-х2), (Х2-х3), . . . (ХM-хM+1) – интервалы (обычно одинаковые по длине), на которые разбивают весь интервал (Х1; хM+1) значений признака Х в выборке, а (N1; N2; . . .; Nm) – частоты для соответствующих интервалов. Например, если исследуется масса Х (г) клубней картофеля, выращенного на некотором поле, то статистическое распределение выборки для 100 клубней, случайно отобранных из выращенного урожая, может быть таким:

	0-40	40-80	80-120	120-160	160-200	(1.4)
	12	20	28	25	15

Графически статистическое распределение выборки вида (1.3) изображается уже не полигоном, а так называемой Гистограммой частот (рис.3.2.):

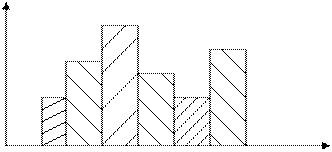Ni

Хi

х1 х2 х3 хM ХM+1

Рис.3.2

Отметим, что часто на оси ординат полигонов и гистограмм откладывают не частоты , а Относительные частоты

Перейдём теперь к основным числовым характеристикам статистического распределения выборки. Ими являются:

1. Среднее значение признака Х в выборке, обозначаемое и называемое Выборочной средней.

2. Величина , которая характеризует Среднее значение квадратов отклонений вариант от выборочной средней . Она называется Выборочной дисперсией.

3. Величина , которая характеризует Среднее значение отклонения вариант от выборочной средней без учёта знака этого отклонения. Она называется Выборочным средним квадратическим отклонением.

4. Величина , называемая Выборочным коэффициентом вариации. Этот коэффициент характеризует Долю в процентах, которую составляет среднее отклонение от среднего по отношению к самому среднему.

Все названные основные числовые характеристики выборки определяются по формулам:

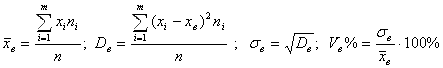(1.5)

Эти формулы можно использовать, если статистическое распределение выборки имеет вид (1.1), то есть является дискретным. А если оно имеет вид (1.3), то есть является непрерывным (интервальным), то его предварительно преобразуют в дискретное, в котором середины интервалов принимаются за его новые дискретные варианты.

Заметим, что введённые выше числовые характеристики выборки введены с той же целью и имеют в принципе тот же смысл, что и числовые характеристики случайных величин – математическое ожидание (среднее значение), дисперсия, среднее квадратическое отклонение, коэффициент вариации, о которых шла речь в курсе теории вероятностей. И названия этих характеристик во многом совпадают.

Кстати, формулу для подсчёта выборочной дисперсии можно упростить, если раскрыть в ней квадрат разности, сумму разбить на три суммы и привести затем подобные. В итоге получим следующую Упрощённую формулу для выборочной дисперсии (выкладки проделайте самостоятельно):

(1.6)

То есть получаем: Выборочная дисперсия равно средней из квадратов вариант выборки минус выборочная средняя в квадрате. Здесь

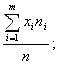
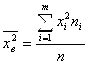= (1.7)

Пример 1. Дано статистическое распределение выборки

	1	2	3	4	(20+15+10+5=N= 50)
	20	15	10	5

Найти , , , .

Решение. Используя приведённые выше формулы, получим:

=

=

Числовые характеристики выборки (, , , ), если они найдены, служат для оценки соответствующих числовых характеристик (, , , ) генеральной совокупности.

Отметим, что числовые характеристики генеральной совокупности – Фиксированные, хотя и неизвестные, числа. А числовые характеристики выборки очевидным образом зависят от того, какие объекты генеральной совокупности попали в выборку. От выборки к выборке эти объекты меняются. А так как выборка объектов производится случайно, то и числовые характеристики выборки – Случайные величины. А значит, возникают естественные вопросы о законах распределения этих случайных величин, их числовых характеристиках и т. д. Обо всём это пойдёт речь в следующем параграфе.

Упражнения

1. В чём достоинства и в чём недостатки исследования всей генеральной совокупности и исследования выборки из неё?

2. Пусть Х – месячная зарплата на сдельной работе одного рабочего на некотором предприятии. Она исследовалась по бухгалтерским ведомостям выборочно. Какой смысл в этом случае будут иметь величины (, , , )? И какой смысл будут иметь (, , , )?

3. Статистическое распределение выборки имеет следующий вид:

	1-3	3-5	5-7	7-9
	20	15	10	5

Найти числовые характеристики выборки.

Ответ: =4; =4; =2; =50%.

< Предыдущая		Следующая >