1.18. Биномиальное распределение

Пусть – число появлений некоторого события в повторных испытаниях, где и – вероятности появления и непоявления этого события в одном испытании. Очевидно, что – дискретная случайная величина, у которой (;;;) – возможные значения, а вероятности (;; ;) этих значений найдутся по формуле Бернулли:

(2.1)

Закон распределения

						(2.2)

Такой случайной величины называется Биномиальным.

Докажем, что математическое ожидание и дисперсия случайной величины , распределенной по биномиальному закону, могут быть найдены по следующим простым формулам:

(2.3)

Для этого представим величину в виде суммы

(2.4)

Здесь – это число появлений события в отдельно взятом -ом испытании . Закон распределения случайной величины при любом номере будет, очевидно, иметь вид:

			(2.5)

Тогда

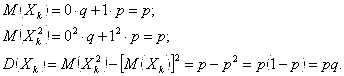(2.6)

Случайные величины (; …) по смыслу своему независимы друг от друга. Поэтому, опираясь на формулы (1.13) и (1.33), получим: (2.7)

Доказательство закончено.

Пример 1. Составить закон распределения случайной величины – числа выпадений герба при трех бросаниях монеты. Найти

Решение. Так как случайная величина Представляет собой число появлений события (выпадения герба) при трех повторных испытаниях (при трех бросаниях монеты), то она имеет биномиальный закон распределения:

Вероятности () найдем по формуле Бернулли (2.1) при и :

Таким образом, для данной биномиально распределенной случайной величины получаем следующий закон распределения:

Ее числовые характеристики найдем с помощью доказанных выше формул (2.3):

< Предыдущая		Следующая >