1.07. Формула сложения вероятностей двух совместных событий

Пусть А и В – любые два совместные события. Геометрически их можно интерпретировать в виде пересекающихся областей А И В соответственно (рис.

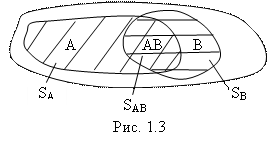(1.3). Заметим, что попадание бросаемой точки в общую часть АВ областей А и В означает появление и события А, и события В, то есть представляет собой произведение АВ событий А и В. Именно поэтому общую часть областей А И В мы обозначили символом АВ.

Рассмотрим и здесь сумму С = А+В событий А и В. Согласно рис. 1.3 вероятность появления события С равна отношению суммарной площади, занимаемой областями А и В, к площади S всей пластинки. Но указанная суммарная площадь равна, очевидно, SА+ SB – SАВ (продумайте это!). Поэтому

P(С) = p(А+В) = (SА+ SB – SАВ)/S = SА/S + SB /S - SАВ/S = p(А)+p(В)-p(АВ).

Таким образом, если А и В – совместные события, то

P(А+В) = p(А)+p(В)-p(АВ) (4.2)

Итак, получаем следующие формулы сложения вероятностей для двух произвольных случайных событий А и В:

p(А+В) = p(А) + p(В) - если А И В несовместны

P(А+В) = p(А)+p(В)-p(АВ) - если А И В совместны (4.3)

< Предыдущая		Следующая >