1.06. Формулы сложения и умножения вероятностей

Формулы сложения и умножения вероятностей – это формулы для нахождения вероятностей сумм и произведений событий. Наиболее просто и наглядно устанавливаются эти формулы с помощью геометрической интерпретации вероятности случайного события, выраженной формулой (1.4) и рисунком (1.1).

1. Формула сложения вероятностей двух несовместных событий.

Пусть А и В – любые несовместные события. Геометрически их можно интерпретировать (изобразить) как попадание брошенной наудачу точки на непересекающиеся одноимённые области А и В соответственно (рис. 1.2):

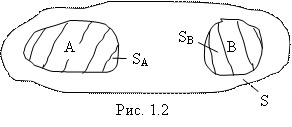Пусть S – площадь всей пластинки, на которую наудачу бросается точка, а SА и SB – площади областей А И В соответственно. Рассмотрим сумму С = А+В событий А И В. По определению суммы событий, событие С состоится в появлении Хотя бы одного из складываемых событий – или А, или В. То есть событие С = А+В состоит в попадании брошенной точки или в область А, или в область В. Следовательно, в соответствии с формулой (1.4) получаем:

P(С) = p(А+В) = (SА+ SB)/S

Но

(SА+ SB)/S = (SА/S)+( SB/S) = p(А)+p(В).

Таким образом, если А И В – несовместные события, то

p(А+В) = p(А) + p(В) (4.1)

< Предыдущая		Следующая >