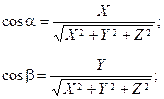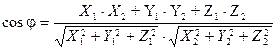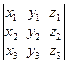Глоссарий
|
№п/п |
Новое понятие |
Содержание |
|
1 |
Алгебраическое дополнение Аij К элементу Аij матрицы третьего порядка А |
|
|
2 |
Алгебраическое дополнение элемента |
Число Aij = (–1)I+J× Mij ,
|
|
3 |
Вектор |
Величина, которая задается числовым значением и напра-влением |
|
4 |
Вектор в n-мерном пространстве |
Упорядоченная совокупность n чисел {X1, X2,…,Xn} |
|
5 |
Векторное произведение |
Вектор 1) 2) 3) тройка векторов |
|
7 |
Канонический базис в n-мерном пространстве |
Векторы |
|
8 |
Квадратная матрица |
Матрица, у которой количество строк равно количеству столбцов |
|
9 |
Коллинеарные векторы |
Векторы, лежащие на параллельных прямых (или на одной и той же прямой) |
|
10 |
Координаты векторного произведения векторов |
|
|
11 |
Линейная комбинация векторов в n-мерном пространстве |
Вектор |
|
12 |
Матрица |
Таблица чисел, состоящая из |
|
13 |
Минор элемента |
Определитель MIj, полученный из матрицы А путем вычеркивания из матрицы i-й строки и j-го столбца |
|
14 |
Модуль векторного произведения |
Численно равна площади параллелограмма, построенного на векторах |
|
15 |
Модуль смешанного произведения |
Численно равен объему параллелепипеда, построенного на векторах |
|
16 |
Направляющие косинусы Вектора |
Косинусы углов, образуемых вектором
|
|
17 |
Определитель det A матрицы второго порядка А
|
|
|
18 |
Определитель det A матрицы третьего порядка |
|
|
19 |
Определитель матрицы |
Число, вычисляемое по определенным правилам с помощью элементов матрицы |
|
20 |
Проекция вектора на ось |
Проекция вектора на ось равна произведению модуля вектора на косинус угла наклона вектора к оси:
|
|
21 |
Произведение вектора |
Вектор, координаты которого равны произведению соответствующих координат вектора L |
|
22 |
Разложение вектора По базисе |
Коэффициенты X, Y, Z в разложении вектора |
|
23 |
Скалярная величина |
Величина, которая может быть задана числом в выбранной систем единиц |
|
24 |
Скалярное произведение вектора |
Число, равное произведению их модулей на косинус угла между ними: |
|
25 |
Скалярное произведение векторов в n-мерном пространстве |
|
|
26 |
Скалярный квадрат вектора |
Скалярным квадратом вектора ( |
|
27 |
Смешанное произведение |
|
|
28 |
Сумма векторов в n-мерном пространстве |
Вектор |
|
29 |
Условие коллинеарности двух векторов, заданных координатами |
Пропорциональность их соответствующих координат: |
|
30 |
Условие компланарности (принадлежности одной плоскости) трех векторов |
Равенство нулю их смешанного произведения: |
|
31 |
Условие перпендикулярности (ортогональности) двух Векторов |
|
|
32 |
Условия равенства двух векторов |
Два вектора равны, если равны соответствующие их координаты |
|
33 |
Формула вычисления скалярного произведения векторов |
|
|
34 |
Формула вычисления угла j между векторами |
|
|
35 |
Формула для вычисления смешанного произведения |
|
|
36 |
Элемент матрицы |
Число |
|
37 |
Элементы главной диагонали |
Элементы матрицы, расположенные на диагонали, идущей из левого верхнего угла матрицы в правый нижний угол, |
|
38 |
Элементы побочной диагонали |
Элементы матрицы, расположенные на диагонали, идущей из правого верхнего угла матрицы в левый нижний угол |
| < Предыдущая | Следующая > |
|---|
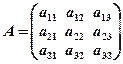

 ;
;