2.6 Операции над векторами, заданными в координатной форме
Прежде всего, заметим, что проекция суммы векторов на любую ось равна сумме проекций слагаемых векторов на ту же ось. Как следствие из этого предложения и определения координат вектора вытекают следующие правила.
1. Два вектора равны, если равны их координаты.
2. При сложении векторов, заданных в координатной форме, их координаты складываются:
Если
![]() ,
, ![]() ,
,
То
![]() . (2.7)
. (2.7)
3. При вычитании векторов, заданных в координатной форме, их координаты вычитаются:
![]() (2.8)
(2.8)
4. При умножении вектора на скаляр надо все его координаты умножить на этот скаляр:
Если
![]() ,
,
То
![]() . (2.9)
. (2.9)
Теперь легко получить Условия коллинеарности двух векторов. Пусть даны два ненулевых коллинеарных между собой вектора ![]() и
и ![]() . Если векторы
. Если векторы ![]() и
и ![]() коллинеарны,
коллинеарны, ![]() ,
, ![]() , то всегда можно найти такой постоянный множитель l ¹ 0, что
, то всегда можно найти такой постоянный множитель l ¹ 0, что ![]() .
.
В координатной форме имеем ![]() .
.
Векторы ![]() и
и ![]() равны, а значит, равны их координаты, следовательно,
равны, а значит, равны их координаты, следовательно,
X1 = lX2, Y1 = lY2,Z1 = lZ2.
Определяя l из каждого из этих трех равенств, можно составить пропорции
![]() . (2.10)
. (2.10)
Полученное равенство является условием коллинеарности двух векторов.
Угол между осью координат и вектором
Углы a, b, g (рисунок 13), образуемые положительными направлениями ОХ, OY, OZ с вектором ![]() {X, Y, X}, можно найти по формулам:
{X, Y, X}, можно найти по формулам:
![]() ; (2.11)
; (2.11)
![]() ; (2.12)
; (2.12)
![]() . (2.13)
. (2.13)
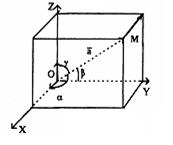
Рисунок 13
Если вектор ![]() единичный, т. е. |
единичный, т. е. |![]() | = 1, то cos a = X, cos b = Y, cos g = Z. Из формул (2.11), (2.12), (2.13) следует, что
| = 1, то cos a = X, cos b = Y, cos g = Z. Из формул (2.11), (2.12), (2.13) следует, что
cos2a + cos2b + cos2g = 1. (2.14)
Величины cosa, cosb, cosg называются Направляющими косинусами вектора ![]() .
.
Пример. Найти направляющие косинусы вектора ![]() {2, –2, –1}.
{2, –2, –1}.
![]()
Деление отрезка в данном отношении
![]() (2.15)
(2.15)
Выразим координаты точки А через концы А1 и А2 и число L.
Распишем векторное равенство (2.15) покоординатно:
X2 – X1 = λ(X – X1); Y2 – Y1 = λ(Y – Y1); Z2 –Z1 = λ(Z – Z1).
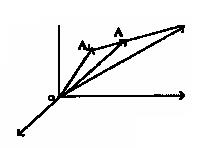
Рисунок 14
Отсюда легко получить искомые координаты:
![]() (2.16)
(2.16)
В частности, координаты середины отрезка А1А2 равны
![]() ,
, ![]() ,
, ![]() . (2.17)
. (2.17)
Заметим, что в случае, если направление вектора ![]() противоположно направлению
противоположно направлению ![]() , то число l < 0.
, то число l < 0.
По формулам (2.16) находим:
![]() .
.
| < Предыдущая | Следующая > |
|---|