2.4 Прямоугольная система координат в пространстве

Три взаимно перпендикулярные оси ОХ, ОY, OZ (рисунок 11), проходящие через некоторую точку O, образуют Прямоугольную систему координат в пространстве.

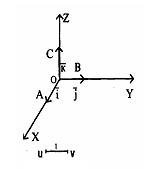
Рисунок 11

Точка О называется началом координат, прямые ОХ, ОY, OZ - осями координат (ОХ – ось абсцисс, ОY – ось ординат, OZ ось аппликат), а плоскости ХОY, YOZ, ZOХ – координатными плоскостями. Какой-либо отрезок UV Принимается за единицу масштаба для всех трех осей. Примем на каждой из осей какое либо направление за положительное. Отложив на осях ОХ, ОY, OZ в положительном направлении отрезки , равные единице масштаба, получим три вектора – орта. Обычно их обозначают следующим образом: . Говорят, что орты Образуют базис трехмерного векторного пространства R3.

Координаты точки. Положение любой точки М в пространстве можно определить тремя чис-лами (координатами) следующим образом: из точки М опустим перпендикуляр MD на плоскость ХОY, затем из точки D опустим перпендикуляр DN На ось ОХ, DL – на ось ОY. Из точки М опустим также перпендикуляр КМ На ось OZ. Числа Х (абсцисса), У (ордината) и Z (аппликата), “измеряющие”, соответственно, отрезки ON, OL и ОК в выбранном масштабе, называются Прямоугольными координатами точки М.

Они берутся положительными или отрицательными в зависимости от того, имеют ли векторы одинаковое либо противоположное направление с ортами . Если точка М имеет координаты X, У, Z, это записывается так: М(Х,У,Z). Вектор , идущий от начала O к некоторой точке М, называется радиус-вектором точки М и обозначается .

Возьмем теперь произвольный вектор , его начало поместим в начало координат О, а конец обозначим буквой М (рисунок 12).

Рисунок 12

Спроектируем теперь вектор = на координатные оси. Величины проекции вектора на координатные оси называются координатами вектора .

Будем обозначать их Х, Y и Z: ПрOx = X, ПрOy = Y, ПрOz = X. Тот факт, что координаты вектора равны Х, Y и Z, записывается следующим образом: = {X, Y, Z}.

Координаты Х, У, Z точки М (конца вектора ), соответственно, равны координатам Х, Y, Z вектора , т. е. X = X, Y = Y, z = Z.

Если два вектора равны, то их координаты соответственно равны, т. е. если и = {X1, Y1, Z1} и = {X2, Y2, Z2}, то X1 = X2, Y1 = Y2, Z1 = Z2.

< Предыдущая		Следующая >