1. Определители. 1.1 Определитель второго порядка
Одним из важных понятий математики является понятие матрицы. Подробное рассмотрение связанных с этим понятием вопросов будет сделано в одной из последующих юнит, где мы разберем операции над матрицами и разберем применение матриц при решении систем линейных уравнений. Здесь мы рассмотрим лишь одно из понятий, относящиеся к теории матриц – понятие Определителя.
При решении некоторых практических задач числа (исходные данные) удобно записывать в виде таблицы, состоящей из N строк и M столбцов. Такую таблицу принято называть Матрицей порядка N ∙ m, а числа, образующие эту таблицу, – Элементами матрицы. Так, например, таблица
![]()
Является квадратной матрицей 2-го порядка (2 строки и 2 столбца). Для общего обозначения произвольного элемента матрицы используется обозначение ![]() , где
, где ![]() - номер строки, в которой находится элемент, а
- номер строки, в которой находится элемент, а ![]() Номер столбца. Для написанной матрицы
Номер столбца. Для написанной матрицы ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В общем случае Квадратную матрицу второго порядка можно записать в виде
. В общем случае Квадратную матрицу второго порядка можно записать в виде
![]() . (1.1)
. (1.1)
Таблица, состоящая из трех строк и трех столбцов,
 (1.2)
(1.2)
Является квадратной матрицей 3-го порядка.
Число ![]() называется элементом матрицы, который находится на пересечении I-й строки и
называется элементом матрицы, который находится на пересечении I-й строки и
j-го столбца; числа I, J называются индексами соответствующего элемента.
В дальнейшем нам придется использовать два следующих понятия, характеризующих любую квадратную матрицу: главная диагональ матрицы и побочная диагональ матрицы. Элементы матрицы, расположенные на диагонали, идущей из левого верхнего угла матрицы в правый нижний угол, называются элементами главной диагонали, а сама эта диагональ называется Главной диагональю матрицы. Элементы матрицы, расположенные на диагонали, идущей из правого верхнего угла матрицы в левый нижний угол, называются элементами побочной диагонали, а сама эта диагональ называется Побочной диагональю матрицы.
Рассмотрим квадратную матрицу 2-го порядка
![]()
Для нее элементы A11, A22 образуют главную диагональ матрицы, а элементы A12, A21 – побочную диагональ.
Для квадратной матрицы третьего порядка
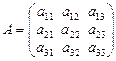
Элементы ![]() образуют главную диагональ, а элементы
образуют главную диагональ, а элементы ![]() - побочную диагональ. Отметим, что у всех элементов главной диагонали номер строки равен номеру столбца.
- побочную диагональ. Отметим, что у всех элементов главной диагонали номер строки равен номеру столбца.
Введем теперь понятие Определителя матрицы второго порядка
![]()
Определителем матрицы А назовем число, соответствующее данной матрице и вычисляемое по следующему правилу:
D = A11 × A22 – A21 × A12. (1.3)
Для вычисления определителя второго порядка из произведения элементов главной диагонали вычитается произведение элементов побочной диагонали.
Его обозначают еще так:
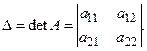
Обозначение det – от слова детерминант, т. е. определитель. Следует обратить внимание на разницу в обозначении матрицы и определителя. Матрица – это таблица, рассматриваемая как единый объект и выделенная круглыми скобками, а определитель – таблица, выделенная вертикальными линиями и дающая в результате вычисления по определенным правилам число.
Например,
![]()
Сделаем два замечания, касающиеся понятия определителя.
Во-первых, определитель – это число, которое ставится в соответствие матрице по специальным правилам.
Во-вторых, определитель можно вычислять только для квадратных матриц, т. е. для матриц, у которых количество строк равно количеству столбцов таблицы.
| Следующая > |
|---|