1.2.3. Уравнение плоскости «в отрезках»
Если мы имеем полное уравнение плоскости (4) и ни один из коэффициентов A, B,C, D не равен нулю, то плоскость (4) пересекает оси координат, и можно найти координаты точек пересечения.
Уравнение Ax + By + Cz + D = 0 запишем в виде
Ax + By + Cz = – D
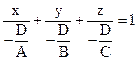 ,
,
Обозначив а= – ![]() , b= –
, b= – ![]() , c= –
, c= – ![]() , получим уравнение плоскости «в отрезках»
, получим уравнение плоскости «в отрезках»
![]() . (5)
. (5)
Легко проверить, что точки M1(a,0,0), M2(0,b,0) и M3(0,0,c), лежащие на координатных осях, удовлетворяют уравнению (5) (рис. 3).
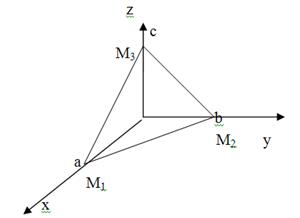
Рис. 3
Точки М1,М2,М3 лежат на трех плоскостях – двух координатных и плоскости (4) и могут быть найдены как решение системы трех линейных уравнений:
Т.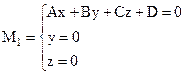 ; т.
; т.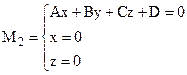 ; т.
; т.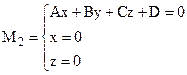 .
.
И вообще, если три плоскости пересекаются в одной точке, то координаты этой точки можно найти, решив систему из трех уравнений (например, по правилу Крамера). Заметим, что две не параллельные плоскости пересекаются по прямой линии, а система двух уравнений имеет бесчисленное множество решений.
| < Предыдущая | Следующая > |
|---|