Приложение 1 - Примеры решения задач и комментарии
Даны координаты вершин треугольника А(0, –2), В(1, 1), С(3, 0). Написать общее уравнение медианы треугольника, опущенной из вершины В.
Решение. Найдем координаты точки М, середины основания АС.
; 
.
Напишем теперь уравнение прямой ВМ, проходящей через две точки В и М:
; 
; 
.
После элементарных преобразований имеем:
или –Y – 1 = 4X – 6, отсюда 4X + Y – 5 = 0.
Получили искомое уравнение медианы.
Даны три точки А(3, 1), В(1, –2), С(3, 4). Написать уравнение прямой, проходящей через точку С перпендикулярно прямой АВ.
Решение. Запишем уравнение прямой АВ, проходящей через две точки А и В.
, или –2(Y – 1) = –3(X – 3), отсюда 2Y – 2 = 3X – 9.
Разрешая это уравнение относительно переменной У, найдем уравнение прямой АВ с угловым коэффициентом:
Угловой коэффициент этой прямой равен 
.
Из условия перпендикулярности двух прямых получим угловой коэффициент К1 прямой, перпендикулярной прямой АВ:
Запишем теперь уравнение прямой с данным угловым коэффициентом К1 и проходящей через точку С. Воспользуемся формулой Y – Yc = K1(X – Xc). Отсюда 
. После элементарных преобразований получаем требуемое уравнение
Пример 3. Заданы две прямые 
и 
.
А. Найти угол между ними.
Б. Провести нормаль к прямой L1 в точке 
. Образуется треугольник, написать уравнение третьей стороны и указать вершины треугольника.
Решение. а. Угол между прямыми L1 и L2 определяется по формуле 
; 
.
Б. Уравнение нормали к прямой L1, проходящей через точку A, имеет вид 
, где 
. Откуда 
, и уравнение нормали 
или 
.
Точка A принадлежит прямым L1 и L3. Надо найти точку пересечения прямых L1 и L2, 
. Откуда 
. Обозначим эту точку 
. А также надо найти точку пересечения прямых L2 и L3. 
. Имеем 
. Обозначим эту точку 
. Таким образом, имеем три вершины треугольника ABC.
Пример 4. Заданы координаты вершин параллелограмма:
.
Написать уравнения всех сторон параллелограмма, определить углы параллелограмма и его площадь.
Решение. Для написания уравнений сторон параллелограмма используем формулу
.
Уравнение стороны AD имеет вид 
, или 
.
Уравнение стороны BC имеет вид 
или 
.
Уравнение стороны AB имеет вид 
, или 
.
Уравнение стороны CD имеет вид 
, или 
.
Угол между прямыми L1 и L2 определим по формуле 
. . Угол между прямыми L3 и L2 
. 
.
Сторона параллелограмма равна 
. Расстояние от точки B до прямой L1 вычисляется по формуле 
. 
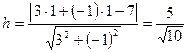. Площадь параллелограмма равна 
.
Пример 5
Дано уравнение второго порядка
9X2 – 4Y2 – 36X – 8Y – 4 = 0.
Написать каноническое уравнение кривой и определить ее тип. Найти полуоси, координаты центра симметрии и фокусы кривой.
Решение. Задача сводится к тому, чтобы привести данное уравнение к одному из следующих видов:
или 
Первое из этих уравнений определяет эллипс, а второе – гиперболу с центром симметрии в точке О(Х0,У0), полуосями A, B (для гиперболы: A – вещественная полуось). Фокусы таких кривых имеют координаты: F1(X0 + C, Y0) и F2(X0 – C, Y0), где C2 = A2 – B2 (для эллипса, если A – большая полуось) и C2 = A2 + B2 (для гиперболы).
Для решения поставленной задачи выделим полные квадраты в следующих выражениях:
9X2 – 36X = 9(X2 - 4X + 4) – 36 = 9(X – 2)2 – 36;
–4Y2 – 8Y = –4(Y2 + 2Y + 1) + 4 = –4(Y + 1)2 + 4.
Подставим теперь полученные выражения в данное уравнение:
9(X – 2)2 – 36 – 4(Y + 1)2 + 4 – 4 = 0 или 9(X – 2)2 – 4(Y + 1)2 = 36.
Поделив обе части уравнения на 36, получим каноническое уравнение гиперболы
Отсюда видно, что центр симметрии гиперболы находится в точке О(2, –1), прямые Х – 2 = 0,
У + 1 = 0 являются ее осями симметрии. Вещественная полуось гиперболы А = 2, мнимая полуось
B = 3, 
Получим координаты фокусов 
.
Дано уравнение кривой в декартовых координатах (X2 + Y2)2 = 4Xy2. Написать это уравнение в полярных координатах.
Решение. Воспользуемся формулами ((1.1), гл. 1) X = R × cos j, Y = R × sin j и подставим эти выражения в данное уравнение.
(R2cos2j + R2sin2j)2 = 4R cos j × R2(sin j)2.
Используя формулы тригонометрии cos2j +sin2j = 1, 2sin j × cos j = sin 2j, получим
R4 = 2R3sin 2j sin j.
Поделим обе части на r3 и получим искомое уравнение
R = 2sin 2j × sin j.
| < Предыдущая |
|---|
