2.3 Эллипс
Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (больше расстояния между фокусами).
Обозначим фокусы эллипса через F1 и F2 (рисунок 2.1), а расстояние между ними через 2С
F1F2 = 2С.
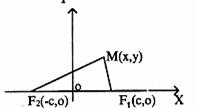
Рисунок 2.1
Примем за ось абсцисс прямую, соединяющую фокусы, выбрав на ней положительное направление от F2 к F1; начало координат возьмем в середине отрезка F1F2 между фокусами. Тогда координаты точек F1 и F2 будут, соответственно, (С, 0) и (–С, 0).
Обозначим сумму расстояний точек эллипса от фокусов через 2А. По определению эллипса имеем
MF1 + MF2 = 2A.
Расписав покоординатно данное равенство, после несложных преобразований получим каноническое уравнение эллипса.
Каноническое уравнение эллипса в выбранной системе координат с данными обозначениями имеет вид
![]() (2.4)
(2.4)
Здесь B2 = А2 – С2 (C < A).
Исследуя уравнение эллипса (2.4), можно сделать следующие заключения относительно формы эллипса.
1. Симметрия эллипса.
Так как уравнение (2.4) содержит только квадраты текущих координат, то если точка (Х, у) находится на эллипсе, то и точки (±X, ±Y) находится на эллипсе при произвольном выборе знаков у координат. Это означает, что оси координат являются осями симметрии эллипса.
Ось симметрии Эллипса, на которой находятся фокусы, называется Фокальной осью. Центр симметрии (точка пересечения осей симметрии) называется Центром Эллипса. Для эллипса, заданного уравнением (2.4), фокальная ось совпадает с осью ОХ, а центр – с началом координат.
Координаты фокусов эллипса, вытянутого вдоль оси X, указаны на рисунке 2.1.
2. Точки пересечения с осями симметрии.
Точки пересечения Эллипса с осями симметрии называются его Вершинами. Вершины А1, А2, В1, В2 эллипса, заданного уравнением (2.4), находятся в точках пересечения эллипса с осями координат. Координаты вершин А1, А2 можно найти, полагая в уравнении (2.4) y = 0:
![]() ,
,
Откуда X2 = А2 и X = ±A.
Полагая X = 0, найдем ординаты вершин B1 и B2:
![]() , или У2 = B2, откуда У = ±B.
, или У2 = B2, откуда У = ±B.
Итак, вершины эллипса имеют следующие координаты:
A1(A, 0), А2(–А, 0), В1(0, B), B2(0, –B) (рисунок 2.2).
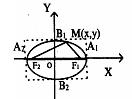
Рисунок 2.2
Отрезки А1А2 = 2А и В1В2 = 2B, соединяющие противоположные вершины эллипса, называются соответственно Большой и малой осями эллипса. Длины А и B называют, соответственно, Большой и малой полуосями эллипса.
3. Форма эллипса.
Из уравнения (2.4) следует, что ![]() , или |X| £ A.
, или |X| £ A.
Аналогично |Y| £ B. Следовательно, эллипс расположен внутри прямоугольника со сторонами, равными 2А и 2B, с центром в начале координат (см. рис.2.2).
Замечание 1. Если A = B (C = 0), уравнение (2.4) принимает вид Х2 + У2 = А2 и определяет окружность, а значит, окружность можно рассматривать как частный случай эллипса с равными полуосями.
Замечание 2. Число ![]() называется Эксцентриситетом Эллипса.
называется Эксцентриситетом Эллипса.
Для эллипса 0 £ e £ 1 (для окружности e = 0). Величина эксцентриситета влияет на форму эллипса. Так, при очень малом e полуоси А и B почти равны и эллипс напоминает окружность. Если же величина e близка к единице, то эллипс имеет сильно вытянутую форму.
Замечание 3. Если фокусы эллипса расположены на оси ОY, то Эллипс «вытягивается» вдоль оси ОY, как это показано на рисунке 2.3, тогда Фокусы Имеют следующие Координаты
F1(0, C) и F2 (0, –C); С2 = B2 – A2; ![]() .
.
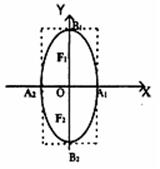
Рисунок 2.3
Как известно, траекторией движения планет и некоторых комет является эллипс, в одном из фокусов которого находится солнце. Оказывается, эксцентриситеты планетных орбит малы, а кометных – велики (близки к 1) – свойство эксцентриситета траекторий планет и комет, где орбиты имеют форму эллипса.
Таким образом, планеты движутся почти по окружностям, а кометы - по вытянутым эллипсам, то приближаясь к солнцу, то удаляясь от него.
Пример 2.2. Составить каноническое уравнение эллипса, зная, что расстояние между фокусами равно 8, а малая полуось B = 3.
Решение. По условию 2C = 8, т. е. C = 4, B = 3.
Мы знаем, что B2 = А2 – С2, отсюда А2 = B2 + С2, т. е. А2 = 32 + 42 = 25 или A = 5.
Уравнение эллипса имеет вид
![]() .
.
Замечание 4. Часто окружность и эллипс задают параметрическими уравнениями.
Параметрическая запись уравнения окружности имеет вид
![]() (2.5)
(2.5)
Для этой окружности центр расположен в точке в точке(0, 0), радиус этой окружности равен R = A.
Параметрическая запись уравнения эллипса имеет вид
![]() . (2.6)
. (2.6)
Центр эллипса расположен в точке(0, 0), а полуоси равны А и B.
| < Предыдущая | Следующая > |
|---|