1. Элементы аналитической геометрии на плоскости. 1.1 Системы координат
Алгебра и геометрия воспринимаются большинством школьников как совершенно разные науки, на самом деле они очень близки. С помощью метода координат можно было бы изложить весь школьный курс геометрии без единого чертежа, используя только Числа и алгебраические операции. Геометрические фигуры при этом описывались бы системами уравнений и неравенств,
а все теоремы геометрии превратились бы в алгебраические соотношения.
Установление связи между алгеброй и геометрией было, по существу, революцией в математике. Это позволило воспринимать математику как единую науку и способствовало ее быстрому развитию. Создателем метода координат считают Рене Декарта, который в последней части философского трактата, вышедшего в 1637 году, дал описание метода координат и его применения к решению геометрических задач. Развитие идей Декарта привело к развитию целой ветви математики, которая решает геометрические задачи аналитически, т. е. алгебраическими методами и методами анализа. Эту часть математики теперь называют аналитической геометрией.
В школьном курсе математики уже было дано определение метода координат. Выберем на плоскости пару Перпендикулярных осей, которые будут Осями координат. Точка пересечения осей является Началом координат. Положение точки М на плоскости относительно введенной системы координат определяется заданием двух чисел: абсциссой Х и ординатой у. Пара чисел
(Х, У) называется Декартовыми прямоугольными координатами точки на плоскости.
Декартова прямоугольная система координат не является единственной системой координат, позволяющей определять положение точек плоскости, но является наиболее простой и часто используемой координатной системой.
Пусть на плоскости даны некоторая точка О (назовем ее Полюсом) и проходящая через нее ось OP (назовем ее Полярной осью) (рисунок 1.1) (Задание полярной системы координат).
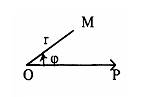
Рисунок 1.1
Положение любой точки М плоскости определяется расстоянием этой точки от полюса – Радиус-вектором r и Полярным углом 
между полярной осью и радиус-вектором R (R – число).
Две координаты (R,J) определяют единственную точку плоскости и называются ее Полярными координатами (условимся придавать радиус-вектору значения R ³ 0, а 0 £ J £ 2P).
Замечание. Полюс О является точкой, радиус-вектор которой равен нулю, а полярный угол не определен.
Таким образом, системы координат позволяют установить Взаимно-однозначное Соответствие между точками плоскости и парами чисел (R, ).
Можно установить связь между декартовыми и полярными координатами одной и той же точки. Пусть даны декартова и полярная системы координат, причем полярная система имеет полюс в начале декартовой системы координат, а полярная ось совпадает с осью абсцисс
(рисунок 1.2).
Рисунок 1.2
Обозначим через Х и У декартовы координаты точки М, через R и ее полярные координаты. Из треугольника OMP вИдно, что Зависимость между полярными координатами (R, ) точки М и ее прямоугольными координатами (Х,У) Выражается формулами:
(1.1)
И обратно,
; 
. (1.2)
Пример 1.1. Даны декартовы координаты точки M(1, –1). Найти ее полярные координаты.
Так как X = 1 > 0 и У = –1 < 0, то точка М находится в IV четверти, а значит 
.
Итак, полярные координаты точки: R = 
, .
| Следующая > |
|---|
