1.3.3 Угол между двумя прямыми

Пусть даны две прямые (рисунок 1.5)

Y = k1X + b1, (I)

у = k2Х + b2. (II)

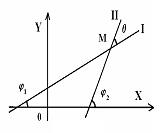
Рисунок 1.5

Углом между прямыми (I) и (II) будем называть тот угол, на который надо повернуть прямую (I) (против часовой стрелки), чтобы она совпадала с прямой (II) (или стала ей параллельна).

Очевидно, что угол между прямыми (I) и (II) определяется не однозначно (с точностью до слагаемого, кратного ). Значение угла всегда можно выбрать так, чтобы оно было неотрицательно и меньше .

Обозначим теперь углы наклона прямых (I) и (II) к оси OX, соответственно, через А угол между прямыми через . Тогда (см. рисунок 1.5) или .

По известной формуле тригонометрии имеем

.

Так как tg j1 = K1 и tg j2 = K2, получим

. (1.10)

Полученная формула является Формулой для вычисления угла между двумя прямыми.

Замечание. Если порядок, в котором рассматриваются прямые, не указан, тогда можно установить его произвольно. Очевидно, изменение порядка повлечет за собой изменение знака для тангенса угла.

Для Вычисления острого угла Q используют формулу .

Пример 1.5. Найти угол между прямыми Y = 2X + 5 и 3X + Y + 2 = 0.

Пронумеруем прямые в порядке их записи, тогда их угловые коэффициенты будут равны
K1 = 2, K2 = –3, соответственно. По формуле (1.10) получим

, отсюда = 45°.

< Предыдущая		Следующая >