15.1. Примеры
Пример 1. Моделирование объема спроса на автомашины.
Наблюдения за объемом продаж автомобилей в салоне «ЛОГОВАЗ» в течение 200 дней показали, что величина спроса изменяется от 0 до 5 автомобилей в день. Частота реализации значений стохастической переменной приведена во втором столбце таблицы:

Постройте модель, позволяющую имитировать значение величины спроса.
Решение. Построим функцию распределения величины спроса и интервалы случайных чисел для значений стохастической переменной. Соответствующие значения указаны в четвертом и пятом столбцах вышеприведенной таблицы.
Сымитируем спрос на автомашины в салоне «ЛОГОВАЗ» в течение 10 последующих дней (случайные числа из таблицы случайных чисел (Приложение 2) выбираем, начиная из верхнего левого угла и двигаясь вниз в первом столбце):

В результате получаем: 39 — спрос за 10 дней; 39/10 = 3,9 — средний ежедневный спрос.
Оценка 3,9 средней величины спроса, полученная в результате имитационного эксперимента, существенно отличается от значения 2,95 — математического ожидания этой случайной величины. Однако эта разница уменьшается с ростом числа испытаний.
Пример 2. Моделирование очереди на разгрузку.
Груженые баржи, отправляемые вниз по Волге из индустриальных центров, достигают Астрахани. Число барж, ежедневно входящих в док, колеблется от 0 до 5. Вероятность прихода 0, 1,..., 5 барж показана в таблице:
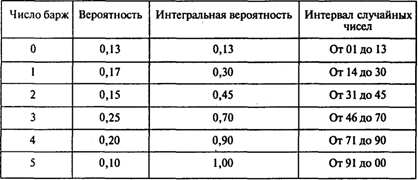
В этой же таблице указаны интегральные вероятности и соответствующие интервалы случайных чисел для каждого возможного значения.
Аналогичная информация дана о числе разгружаемых барж:
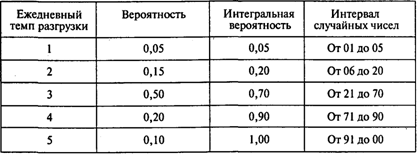
Постройте модель, позволяющую имитировать очередь на разгрузку.
Решение. Проведем эксперимент, имитирующий очередь на разгрузку барж в порту Астрахани:

Окончание таблицы
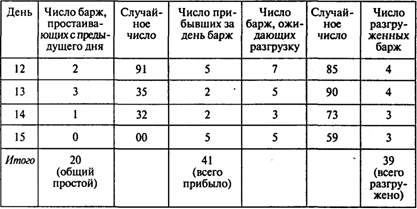
В результате эксперимента получены:
Оценка среднего числа барж, простаивающих в течение суток, равная 20/15;
Оценка среднего числа барж, прибывающих в течение суток, равная 41/15;
Оценка среднего числа барж, разгруженных в течение суток, равная 39/15.
Пример 3. Имитация стратегии резервирования.
Магазин электрооборудования продает электрические дрели. В течение 300 дней директор магазина Проводков регистрировал дневной спрос на дрели. Распределение вероятностей величины спроса показано в таблице:
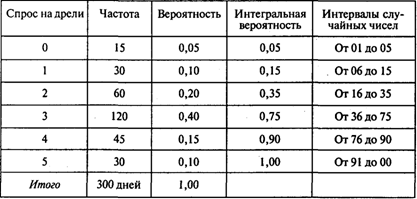
Когда Проводков делает заказ, чтобы возобновить свои запасы электрических дрелей, его выполнение происходит с лагом в 1, 2 или 3 дня. Это означает, что время восстановления запаса подчиняется вероятностному распределению. В следующей таблице указаны сроки, вероятности сроков выполнения заказов и интервалы случайных чисел, которые удалось определить на основе информации о 50 заказах:

Стратегия резервирования, которую хочет имитировать Проводков, — делать заказ в объеме 10 дрелей при запасе на складе 5 шт. Проводков оценил, что каждый заказ на дрели обходится ему в 10 руб., хранение каждой дрели — в 5 руб. в день, одна упущенная продажа — в 80 руб. Цель эксперимента — оценить величину средних ежедневных затрат для этой стратегии управления запасами.
Решение. Реализуется четырехшаговый процесс имитации:
1. Каждый имитируемый день начинается с проверки, поступил ли сделанный заказ. Если заказ выполнен, то текущий запас увеличивается на величину заказа (в данном случае — на 10 единиц).
2. Путем выбора случайного числа генерируется дневной спрос для соответствующего распределения вероятностей.
3. Рассчитывается итоговый запас, равный исходному запасу за вычетом величины спроса. Если запас недостаточен для удовлетворения дневного спроса, спрос удовлетворяется, насколько это возможно. Фиксируется число нереализованных продаж.
4. Определяется, снизился ли запас до точки восстановления (в примере — 5 единиц). Если да, причем не ожидается поступления заказа, сделанного ранее, то делается заказ.
Первый эксперимент Проводкова (объем заказа — 10 шт., точка восстановления запаса — 5 шт.; СЧ — случайное число):
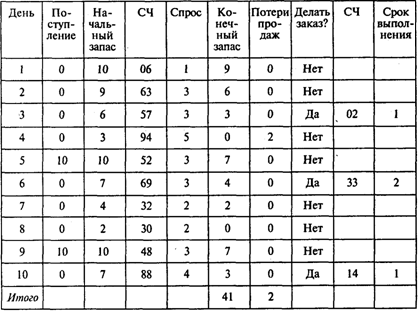
Результат имитационного эксперимента:
Конечный суммарный запас — 41 единица;
Средний конечный запас 41/10 =4,1 единицы;
Число упущенных продаж — 2;
Среднее число упущенных продаж 2/10 = 0,2 шт. в день;
Среднее число заказов 3/10 = 0,3 заказа в день.
Определим три составляющие затрат:
Ежедневные затраты на заказы = Затраты на один заказ х Среднее число заказов в день = 10 • 0,3 = 3 руб.
Ежедневные затраты на хранение = Затраты на хранение одной единицы в течение дня х Средняя величина конечного запаса = 5 • 4,1 = 20,5 руб.
Ежедневные упущенные продажи = Прибыль от упущенной продажи х Среднее число упущенных продаж в день = 80 • 0,2 = 16 руб.
Таким образом,
Общие ежедневные затраты = Затраты на заказы + Затраты на хранение + Упущенные продажи = 3 + 20,5 + 16 = 39,5 руб.
| < Предыдущая | Следующая > |
|---|