07. Задача о назначениях
Цели
В процессе управления производством зачастую возникают задачи назначения исполнителей на различные виды работ, например: подбор кадров и назначение кандидатов на вакантные должности, распределение источников капитальных вложении между различными проектами научно-технического развития, распределение экипажей самолетов между авиалиниями.
Задачу о назначениях можно сформулировать следующим образом. Необходимо выполнить N различных работ. Для их выполнения можно привлечь N рабочих. Каждый рабочий за определенную плату готов выполнить любую работу. Выполнение любой работы следует поручить одному рабочему. Требуется так распределить работы между рабочими, чтобы общие затраты на выполнение всех работ были минимальными.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь определять и использовать для экономического анализа:
• задачу о назначениях в стандартной форме;
• открытую задачу о назначениях;
• таблицу задачи о назначениях;
• матрицу назначений;
• эффективность назначений.
Модели
Пусть Т — количество работ.
Задача о назначениях в стандартной форме. При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих Равно количеству работ.
Обозначения:
СIj — показатель эффективности назначения I-го рабочего на J-й работе, например издержки выполнения I-М рабочим J-й работы;
Xij — переменная модели (ХIj = 1, если I-й рабочий используется на J-й работе, и Xij = 0 в противном случае).
Модель задачи о назначениях:
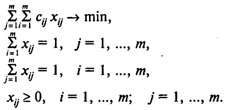
![]()
Здесь (1) — целевая функция (минимум издержек на выполнение всех работ);
(2) — система ограничений, отражающая следующие условия:
А) каждая работа должна быть выполнена одним рабочим;
Б) каждый рабочий может быть привлечен к одной работе;
(3) — условия неотрицательности переменных.
При решении задачи о назначениях исходной информацией является таблица задачи о назначениях с={СIj}, элементами которой служат показатели эффективности назначений. Для задачи о назначениях, записанной в стандартной форме, количество строк этой таблицы совпадает с количеством столбцов:

Результатом решения задачи о назначениях (1)—(3) является вектор Х* = {![]() }, компоненты которого — целые числа.
}, компоненты которого — целые числа.
Оптимальный план задачи о назначениях (1)—(3) можно представить в виде квадратной матрицы назначений, в каждой строке и в каждом столбце которой находится ровно одна единица. Такую матрицу иногда называют матрицей перестановок. Значение целевой функции (1), соответствующее оптимальному плану, называют Эффективностью назначений.
Задача о назначениях в открытой форме. Задача о назначениях в открытой форме возникает тогда, когда количество рабочих Не равно количеству работ. В этих случаях задача может быть преобразована в задачу, сформулированную в стандартной форме.
Пусть, например, количество рабочих П превышает количество работ Т.
Введем дополнительные фиктивные работы с индексами J = W + 1,..., П. Коэффициенты таблицы назначений СIj , I = 1,..., П; J = т + 1,..., П, положим равными нулю. В этом случае получаем задачу, сформулированную в стандартной форме. Если в оптимальном плане этой задачи ![]() = 1 при J = Т + 1,..., П, то исполнитель I назначается на выполнение фиктивной работы, т. е. остается без работы. Заметим, что оптимальное значение целевой функции исходной задачи совпадает с оптимальным значением задачи, приведенной к стандартной форме. Поэтому эффективность назначений в результате такого преобразования не меняется.
= 1 при J = Т + 1,..., П, то исполнитель I назначается на выполнение фиктивной работы, т. е. остается без работы. Заметим, что оптимальное значение целевой функции исходной задачи совпадает с оптимальным значением задачи, приведенной к стандартной форме. Поэтому эффективность назначений в результате такого преобразования не меняется.
Следует особо отметить, что задача о назначениях является частным случаем транспортной задачи, в которой количество пунктов производства совпадает с количеством пунктов потребления, а все величины спроса и величины предложения равны.
| < Предыдущая | Следующая > |
|---|