07.3. Задачи
Задача 1. Цех металлообработки получил срочный заказ на выпуск партии деталей. Для производства детали необходимо выполнить операции на четырех станках. В цехе работают четыре слесаря высокой квалификации, каждый из которых может работать на любом станке, но с различным процентом брака (процент брака известен из документации ОТК):
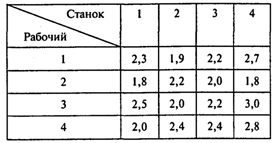
Распределите станки между рабочими таким образом, чтобы процент брака был минимальным. (Предполагается, что ОТК проверяет готовую деталь, т. е. общий процент брака определяется как сумма процентов брака, допущенного всеми рабочими.)
Вопросы:
1. На каком станке должен работать рабочий 2?
2. Чему равен минимальный общий процент брака?
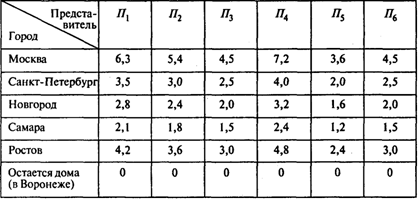
Задача 2. Воронежская фирма по производству мужских головных уборов планирует освоение новых рынков сбыта в пяти городах. Возможности сбыта невелики, так что в каждый город достаточно направить одного торгового представителя фирмы для заключения с магазинами договоров о поставках.
В следующей таблице указан объем спроса (в млн руб.):

Фирма располагает данными о профессиональных возможностях шести своих сотрудников. В следующей таблице содержатся оценки степени освоения рынка, которую может обеспечить соответствующий торговый представитель фирмы:

Так, представитель П1 может освоить 70% от объема спроса в любом городе. Например, если направить его в Москву, то доход фирмы на этом рынке составит 6,3 млн руб.
Распределите торговых агентов по городам таким образом, чтобы фирма получила максимальный доход.
Вопросы:
1. Чему равен максимальный доход фирмы?
2. В какой город следует направить торгового представителя П1?
3. Кто из торговых представителей не будет использован?
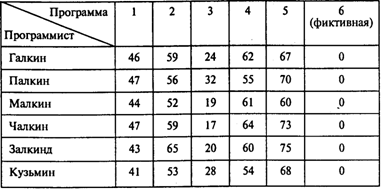
Задача 3. Фирма получила заказы на разработку пяти программных продуктов. На фирме работают шесть квалифицированных программистов, которым можно поручить выполнение этих заказов. Каждый из них дал оценку времени (в днях), требуемого для разработки программ. Эти оценки приведены в следующей таблице:
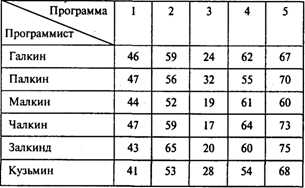
Выполнение каждого из пяти заказов фирма решила поручить одному программисту. Ясно, что один из программистов не получит заказа.
Каждому программисту, которому будет поручено выполнять заказ, фирма предложила оплату 1 тыс. руб. в день. Распределите работу между программистами, чтобы общие издержки на разработку программ были минимальными.
Вопросы:
1. Чему равны минимальные издержки фирмы на выполнение всех пяти заказов?
2. Какую программу следует поручить Малкину?
3. Какую программу следует поручить Залкинду?
4. Кто из программистов не получит заказа?
5. Стало известным, что не все программисты согласились с условиями оплаты, обосновывая это тем, что имеют разную квалификацию. В результате была достигнута договоренность о следующих размерах оплаты в день (в тыс. руб.):

Изменится ли распределение работ между программистами при новых условиях оплаты труда? Каковы будут в этом случае общие минимальные издержки? б. Кто из программистов при новых условиях не получит заказа?
Задача 4. Пять учебных групп экономического факультета МГУ собираются посетить во время практики 10 предприятии и НИИ. Каждая учебная группа может посетить две организации. Путем опроса студентов выявлены предпочтения каждой группы для 10 организаций (1 означает «наиболее предпочтительна», а 10 — «наименее предпочтительна»). Предпочтения каждой из пяти учебных групп показаны в таблице (П-1 ¸ П-5 — промышленные предприятия; НИИ-1 ¸ НИИ-5 — научно-исследовательские институты):
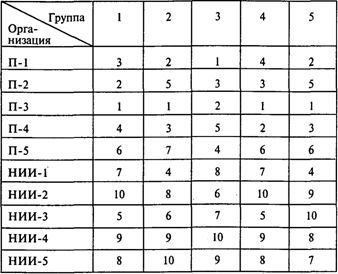
Определите, какие две организации должна посетить каждая группа, чтобы в максимальной степени были учтены предпочтения всех студентов.
Вопросы:
1. Чему равна сумма баллов, соответствующая наилучшему распределению групп по организациям?
2. Какая группа должна посетить НИИ-2?
3. Какую еще организацию должна посетить эта группа?
4. Деканат внес предложение, чтобы каждая группа посетила одно предприятие и один НИИ. Укажите теперь такой вариант распределения, чтобы каждой группе досталось по одному промышленному предприятию и одному НИИ. Чему равна сумма оценочных баллов в этом случае?
5. Какая группа должна посетить НИИ-5 при новых условиях?
6. Какую еще организацию должна посетить эта группа?
Задача 5. Самолеты компании «Аэрофлот» летают между Москвой и Сочи. Полеты беспосадочные. График движения показан в следующей таблице:
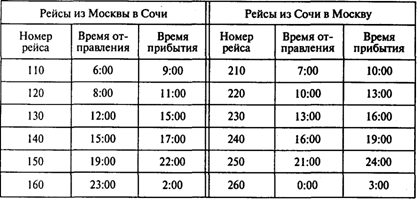
Рейсы могут обслуживаться московскими или сочинскими экипажами. Любой экипаж выполняет пару рейсов — «туда и обратно». Время, необходимое для подготовки самолета к очередному рейсу, — один час. Требуется определить, какую пару рейсов следует выполнять каждому экипажу и из какого отряда, московского или сочинского, должен быть соответствующий экипаж. Распределение рейсов необходимо осуществить таким образом, чтобы суммарное время ожидания вылета в «чужом» городе было минимальным. Время ожидания не включает тот час, который уходит на подготовку самолета к очередному рейсу.
Вопросы:
1. Верно ли, что рейс 210 должен выполняться московским экипажем?
2. Верно ли, что рейсы 240 и 160 должны выполняться одним экипажем?
3. Верно ли, что рейс 160 должен обслуживаться сочинским экипажем?
4. Каково минимальное общее время пребывания экипажей в «чужих» городах?
5. Какое количество рейсов должны выполнять московские экипажи?
Ответы и решения
Ответы на вопросы: 1—1, 2 — 2, 3—5, 4 — 3, 5 —3.
Задача 1. Решение.
Таблица задачи о назначениях представлена в условии. Проводя оптимизационные расчеты, получаем следующую матрицу назначений:
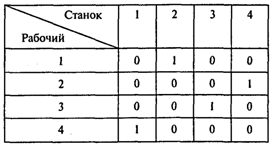
Решение можно представить в следующем виде:
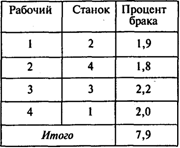
Ответы: 1. На станке 4. 2. 7,9%.
Задача 2. Решение.
Способ 1 (без проведения оптимизационных расчетов). Известно, что при любых неотрицательных А1, B1, а2, B2 соотношение А1B1 + А2B2 ³ а2B1 + А1B2 выполняется в случае, когда A1 ³ а2, и B1 ³ B2. Используя это утверждение, можно показать, что максимальный доход будет в том случае, когда торговый представитель, обеспечивающий максимальную долю освоения рынка, будет направлен в город с максимальным объемом спроса, и т. д.
Способ 2. В таблице задачи о назначениях указан размер дохода (в млн руб.), который можно получить при направлении представителя фирмы в соответствующий город:
Проводя оптимизационные расчеты, получаем следующий результат:

Ответы: 1. 17,9 млн руб. 2. В Ростов. 3. Представитель П5.
Задача 3. Решение.
В таблице задачи о назначениях указан размер оплаты (в тыс. руб.) в случае, если программисту будет поручена соответствующая программа:
Проводя расчеты, получаем следующую матрицу назначений:

Учитывая исходную информацию, получаем следующий результат:
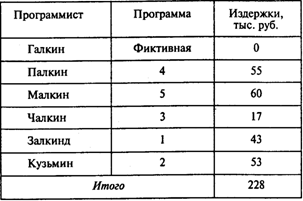
Из последней таблицы следует, что минимальные издержки составляют 228 тыс. руб., Малкину следует поручить программу 5, а Залкинду — программу 1. Заказа не получит Галкин.
При Новых условиях оплаты труда таблица задачи о назначениях имеет следующий вид:
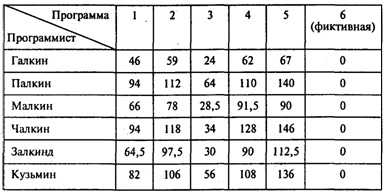
Проводя расчеты, получаем следующую матрицу назначений:
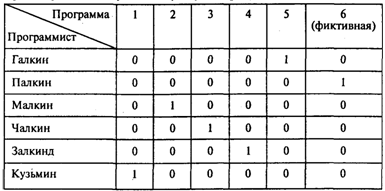
В следующей таблице приведен итоговый результат:

Ответы: 1. 228 тыс. руб. 2. Программу 5. 3. Программу 1. 4. Программист Галкин. 5. 351 тыс. руб.
6. Программист Палкин.
Задача 4. Решение.
В таблице задачи о назначениях указаны предпочтения каждой группы, при этом каждая группа представлена дважды, так как может посетить две организации:
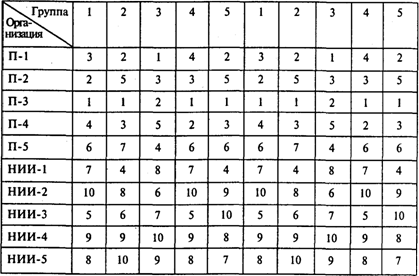
Проводя оптимизационные расчеты, получаем следующий результат:

Если учесть предложение деканата, то надо решить две задачи о назначениях: сначала распределить группы по предприятиям, затем — по НИИ. Эти две задачи можно представить в виде одной оптимизационной задачи, имеющей следующую таблицу (М— большое число):
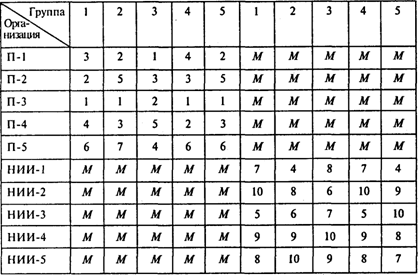
Минимизируя общую сумму баллов, получаем следующую матрицу назначений:

Ответ можно представить в виде следующей таблицы:

Ответы: 1. 41. 2. Группа 3. 3. Предприятие П-5. 4. 42. 5. Группа 5. 6. Предприятие П-1.
Задача 5. Решение.
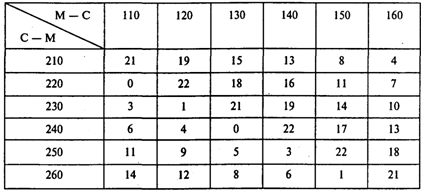
Составляем таблицу задачи о назначениях, предполагая, что все рейсы выполняются московскими экипажами. Наименование столбца таблицы — номер рейса «Москва — Сочи» (М — С). Наименование строки — номер обратного рейса «Сочи — Москва» (С — М). В таблице для каждой возможной пары рейсов, выполняемых одним экипажем, указано время ожидания вылета в Сочи (в часах):
Московский экипаж
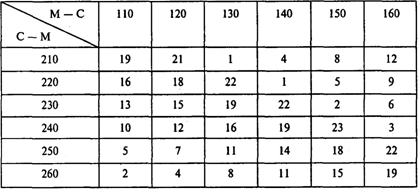
Составляем таблицу задачи о назначениях, предполагая, что все рейсы выполняются сочинскими экипажами. Наименование строки — номер рейса «Сочи — Москва». Наименование столбца — номер обратного рейса «Москва — Сочи». В таблице для каждой возможной пары рейсов, выполняемых одним экипажем, указано время ожидания вылета в Москве (в часах):
Сочинский экипаж
Составляем итоговую таблицу задачи о назначениях. Учитываем, что каждая пара рейсов может выполняться либо московским, либо сочинским экипажем. Поэтому в итоговую таблицу включаем минимальные значения времени ожидания (в часах) из двух приведенных выше таблиц:
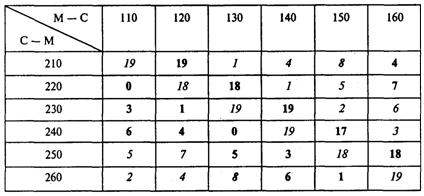
Элементы, выделенные полужирным шрифтом, взяты из таблицы для московского экипажа. Соответствующие пары рейсов должны выполняться московским экипажем. Элементы, выделенные курсивом, взяты из таблицы для сочинского экипажа. Соответствующие пары рейсов должны выполняться сочинским экипажем. Элементы, выделенные полужирным курсивом, показывают, что соответствующая пара рейсов может выполняться экипажем, приписанным к любому из двух городов.
Решая задачу, получаем следующую матрицу назначений:
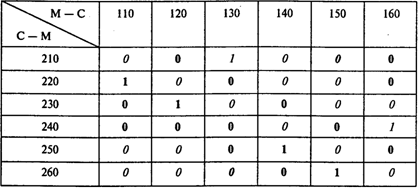
В матрице назначений единица, выделенная полужирным шрифтом, означает, что соответствующая пара рейсов должна выполняться московским экипажем. Единица, выделенная курсивом, означает, что соответствующая пара рейсов должна выполняться сочинским экипажем.
В итоге получаем следующее решение задачи:
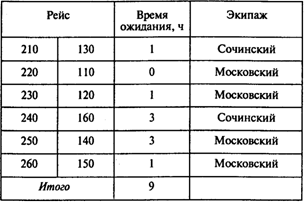
Ответы: 1. Нет, рейс 210 должен выполняться сочинским экипажем. 2. Да. 3. Да. 4. 9 часов. 5. Восемь рейсов.
| < Предыдущая | Следующая > |
|---|