06. Транспортная задача
Цели
В данной главе рассматривается задача транспортировки продукта, который в определенных количествах предлагается различными производителями. Известны потребности нескольких потребителей в этом продукте. Требуется определить, от каких производителей и в каких объемах должны получать продукт потребители. Поставки должны осуществляться таким образом, чтобы совокупные издержки на транспортировку продукта были минимальными.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь составлять и использовать для экономического анализа:
• замкнутую и открытую транспортные задачи;
• транспортную задачу с запретами;
• транспортную задачу с фиксированными перевозками;
• транспортную задачу с ограничениями на пропускную способность;
• транспортную задачу с фиксированными доплатами;
• транспортную таблицу.
Модели
Обозначения:
АI — величина предложения продукта в пункте I (I = 1, ..., N);
Bj — величина спроса на продукт в пункте J (J = 1,..., Т);
Cij — затраты на транспортировку единицы продукта из пункта I в пункт J;
Xij — количество продукта, перевозимого из пункта I в пункт J.
Модель транспортной задачи:
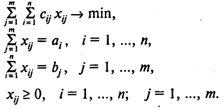
![]()
Здесь (1) — целевая функция (минимум затрат на транспортировку продукта);
(2) — ограничения по величине предложения в каждом пункте производства;
(3) — ограничения по величине спроса в каждом пункте потребления;
(4) — условия неотрицательности объемов перевозок.
1. Замкнутая транспортная задача. Общее предложение Равно Общему спросу:
![]()
Это необходимое и достаточное условие существования допустимого плана задачи (1)—(4).
2. Открытая транспортная задача.
А) ![]() — Излишек продукта
— Излишек продукта
Способ сведения к замкнутой задаче. Пусть Bm+1 — величина избытка продукции, т. е. ![]() - штраф за единицу продукта, не реализованного в пункте I; УI — количество продукта, не реализованного в пункте I.
- штраф за единицу продукта, не реализованного в пункте I; УI — количество продукта, не реализованного в пункте I.
Замкнутая транспортная задача имеет вид
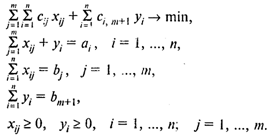
Б) ![]() — Дефицит продукта.
— Дефицит продукта.
Способ сведения к замкнутой задаче. Пусть АN+1 — величина дефицита продукции, т. е. ![]() - штраф за единицу продукта, недопоставленного в пункт J; УJ — количество продукта, недопоставленного в пункту.
- штраф за единицу продукта, недопоставленного в пункт J; УJ — количество продукта, недопоставленного в пункту.
Замкнутая транспортная задача имеет вид
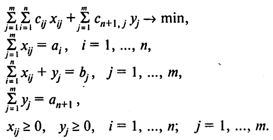
3. Транспортная задача с запретами. Пусть Е — множество пар индексов (Ij), таких, что из пункта I в пункт J допускается транспортировка продукта. Между любыми другими двумя пунктами транспортировка не допускается.
Пусть М— большое число, например
![]()
Тогда ![]()
В оптимальном плане {![]() } транспортной задачи
} транспортной задачи ![]() при ограничениях (2)—(4) Xij = 0, если (I,J) Ï Е.
при ограничениях (2)—(4) Xij = 0, если (I,J) Ï Е.
4. Транспортная задача с фиксированными перевозками. Если объем перевозок между пунктами I и J задан, то в задаче (1)—(4) вводится дополнительное ограничение: Xij = Vij, где Vij — заданный объем перевозок.
5. Транспортная задача с ограничениями на пропускную способность. Если объем перевозок из пункта I в пункт J ограничен величиной Wij, то в задаче (1)—(4) вводится дополнительное ограничение: Xij £ Wij.
6. Транспортная задача с фиксированными доплатами. Предположим, что в открытой транспортной задаче имеет место дефицит продукта и для его устранения в пунктах I = п + 1, ..., K возможно создание новых мощностей Di.
Пусть переменные Zi = 1, если в пункте I (I = П + 1, ..., K) вводятся мощности Di и Zi = 0, если в пункте I мощности не вводятся. Издержки на ввод мощностей D, в пункте I (I = N + 1, ..., K) составляют ИI.
С учетом возможности создания новых мощностей транспортная задача может быть записана в следующем виде:
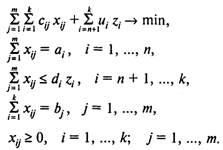
![]()
Здесь (5) — целевая функция (минимум затрат на транспортировку и ввод мощностей);
(6) — ограничения по величине предложения в каждом существующем пункте производства;
(7) — ограничения по величине предложения в каждом новом пункте производства;
(8) — ограничения по величине спроса в каждом пункте потребления;
(9) — условия неотрицательности объемов перевозок.
Помимо непрерывных переменных Xij в модель включены булевы переменные Zi,. Задача (5)—(9) является задачей линейного программирования со «смешанными» переменными.
Все приведенные модели описывают транспортную задачу в виде задачи линейного программирования. В такой форме она может быть решена стандартными средствами линейного программирования, например симплекс-методом.
Для решения транспортной задачи могут быть использованы также и менее трудоемкие (по объему вычислений) алгоритмы, например метод потенциалов.
Большинство специальных алгоритмов решения транспортной задачи использует исходную информацию в форме транспортной таблицы:
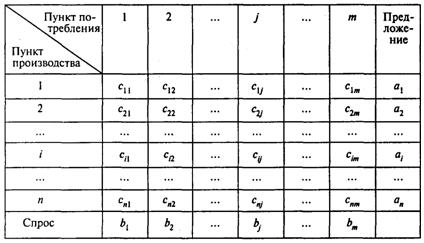
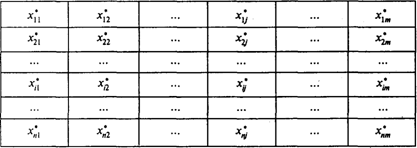
Оптимальный план перевозок имеет вид
| < Предыдущая | Следующая > |
|---|