05. Планирование финансов

Цели

В данной главе показаны возможности использования Модели линейного программирования для решения некоторых задач плани­рования финансов. При определенных предположениях становит­ся возможным выбрать такие способы вложения денег под процен­ты, совокупность которых позволяет минимизировать первоначаль­ный вклад, необходимый для выплаты займа, или максимизировать доход. При решении задач финансового планирования можно учи­тывать риск и другие факторы, влияющие на выбор способов вло­жения денег.

После выполнения заданий, предлагаемых в этой главе, вы бу­дете уметь формулировать и использовать для экономического анализа следующие понятия:

• вклад;

• целевой фонд;

• балансовое ограничение;

• индекс риска по вкладу.

Модели

Модель А минимизации целевого фонда. Предположим, что в определенные моменты времени необходимо выплачивать извест­ные суммы денег по взятому ранее займу. Чтобы накопить эти суммы, можно заранее создать целевой фонд, а средства из этого фонда использовать для срочных вкладов. Каждый срочный вклад характеризуется моментом времени вложения, сроком погашения и доходностью. Задача состоит в том, чтобы определить минималь­ный размер целевого фонда и выбрать те виды срочных вкладов, которые следует использовать, чтобы сделать выплату по займу. Обозначения:

У — размер целевого фонда, создаваемого в нулевой момент времени;

T — текущий момент времени, T = 0, 1,.... Т;

Dt — размер выплаты по займу, которую надо произвести в мо­мент времени T (T = 1, ..., Т);

J —индекс срочного вклада, J = 1,..., П;

Vj — момент времени вложения по срочному вкладу J;

Wj — срок выплаты по срочному вкладу J;

Rj — доходность срочного вклада J (процент по вкладу);

ХJ — объем вложений по срочному вкладу J.

Предполагается, что для любого срочного вклада J момент VJ Времени вложения фиксирован. Если по срочному вкладу/сде­ланы вложения в размере ХJ, то через WJ единиц времени вклад­чику выплачивается сумма (1 + Rj)хJ. Без ограничения общности можно считать, что для любого момента времени существует та­кой вклад, выплата по которому производится в следующий мо­мент времени. При этом доходность такого вклада может быть нулевая. Использование вклада с нулевой доходностью означает, что деньги остаются на руках у владельца.

Пусть Gt — множество индексов J, таких, что T= Vj, т. е. по вкладу J сделано вложение в момент времени T, Qt — множество индексов J, таких, что T = vJ + WJ, т. е. по вкладу J получена выплата в момент времени T.

Заметим, что для любого T множества Gt и Qt известны.

Тогда модель имеет следующий вид:

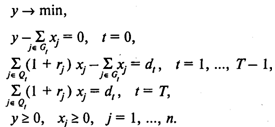
Здесь (1) — целевая функция (минимальный размер целевого фонда);

(2) —условие, характеризующее распределение целевого фонда по вкладам в нулевой момент времени;

(3) — соотношения, устанавливающие баланс между выпла­тами и вложениями;

(4) — условие, обеспечивающее выплату по займу;

(5) — условия неотрицательности переменных.

Модель В максимизации дохода. Предположим теперь, что вкладчик собирается делать вклады для того, чтобы через опреде­ленный период времени получить максимальный доход. Задача состоит в том, чтобы определить величину максимального дохода при фиксированном размере целевого фонда и выбрать те виды срочных вкладов, которые следует использовать.

Сохраним принятые ранее обозначения и введем новые:

Z — размер дохода, который может получить вкладчик в мо­мент времени Т;

ИT— размер вклада в момент времени T (T = 0, 1,..., Т— 1).

Тогда модель имеет следующий вид:

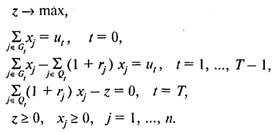
Здесь (6) — целевая функция (максимальная величина дохода);

(7) — условие, характеризующее распределение вклада в нулевой момент времени;

(8) — соотношения, устанавливающие баланс между вы­платами и вложениями;

(9) — условие, определяющее величину дохода;

(10)—условия неотрицательности переменных.

< Предыдущая		Следующая >