04.4. Ответы и решения

Ответы на вопросы: 1—5, 2 — 4, 3—3, 4—2, 5 — 1.

Задача 1. Решение.

Определим все рациональные способы раскроя прямоугольного листа железа размером 100 х 60 см на квадратные заготовки со сторонами 50, 40 и 20 см.

Получаем шесть рациональных способов раскроя:

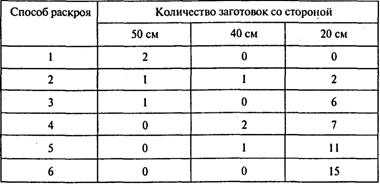
Пусть Х1, ..., х6 — количество единиц материала, раскроенных соответству­ющим способом, Х7 — количество изготовленных коробок. Тогда ответ на второй вопрос можно получить, используя следующую модель:

Проводя расчеты, получаем следующий результат:

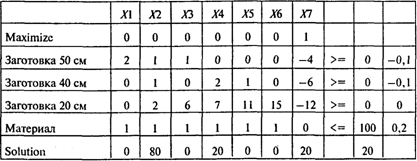
Отсюда следует, что из 100 листов железа можно изготовить 20 ящиков. При этом следует использовать два способа раскроя.

Значение двойственной оценки показывает, что при увеличении количества материала на один лист можно дополнительно изготовить 0,2 коробки.

В следующей таблице приведены границы устойчивости:

Учитывая границы устойчивости по ограничению «материал», можно сделать вывод, что для изготовления одной коробки требуется пять листов железа.

Ответы: I. Шесть способов. 2. 20 коробок. 3. Два способа. 4. Пять листов.

Задача 2. Решение.

Заметим, что всего существует пять рациональных способов раскроя.

Пусть Х1, ..., Х5 — количество единиц материала, раскроенных соответству­ющим способом, Х6 — количество комплектов. Тогда используем следующую модель:

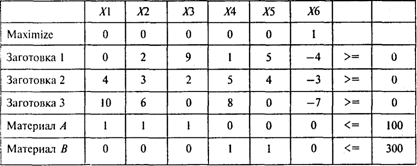
Решая эту задачу, получаем следующий результат:

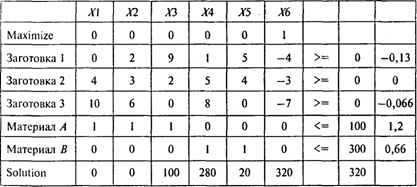
Используется три рациональных способа раскроя из пяти. Из имеющегося материала можно изготовить 320 комплектов заготовок. Третьим способом сле­дует раскраивать все 100 единиц материала А. Для ответа на последний вопрос задачи увеличим количество заготовок в комплекте с 3 до 7. Получим следующий результат:

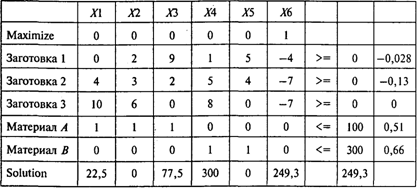
Ответы: 1. Три способа. 2. 320 комплектов. 3. 100 единиц. 4. 249 комплектов.

Задача 3. Решение.

Предположим, что на фабрику поступает 100 м ткани 2. Тогда ткани 1 посту­пает 200 м. Модель оптимального раскроя будет иметь следующий вид:

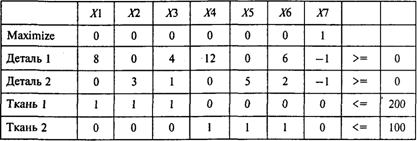
Проводя расчеты, получаем следующий результат:

Предположим, что оба вила ткани поступают в равных количествах. Тогда при условии, что общее количество ткани остается неизменным, получаем следующую модель оптимального раскроя:

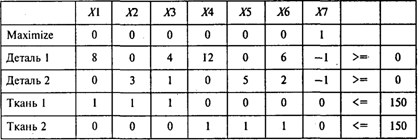
Проводя расчеты, получаем следующий результат:

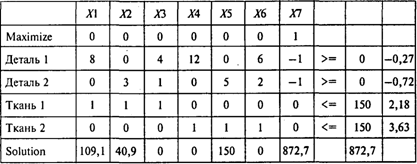
Ответы: 1. Два способа. 2.50%. 3. На 9%.

Задача 4. Решение.

Определяем рациональные способы раскроя материала каждого вида на заго­товки. Получаем пять способов, показанных в следующей таблице:

Задача минимизации отходов при условии выполнения задания по изготов­лению заготовок описывается следующей моделью:

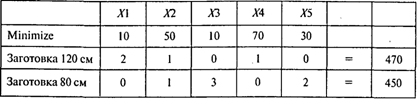
Проводя расчеты, получаем следующий результат:

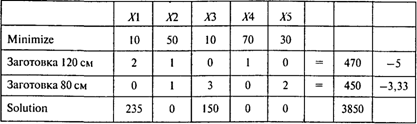
При условии, что количество материала длиной 250 см ограничено, получа­ем модифицированную модель:

Проводя расчеты, получаем следующий результат:

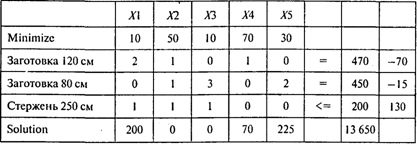
Ответы: 1. 385 стержней. 2. 0. 3. 3850см. 4. 295 стержней. 5. На 9800 см.

Задача 5. Решение.

Определяем рациональные способы раскроя материала каждого вида на заго­товки. Получаем девять способов, показанных в следующей таблице:

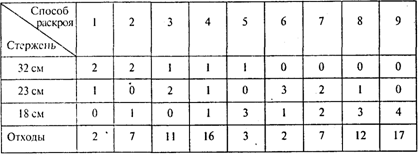
Задача максимизации количества комплектов при ограничении на количество используемого материала описывается следующей моделью:

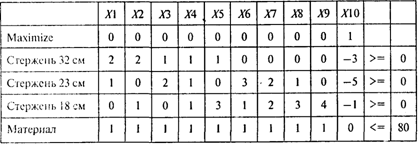
Проводя расчеты, получаем следующий результат:

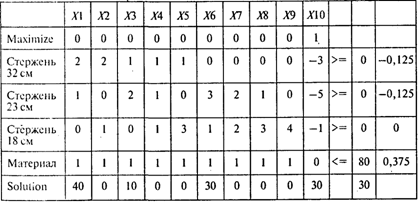
Ответы: 1. Девять способов. 2. 30 комплектов. 3. 250см.

< Предыдущая		Следующая >