04. Оптимальный раскрой
Цели
В данной главе показаны возможности использования Модели линейного программирования Для решения задач раскроя. Эта область приложения модели линейного программирования хорошо изучена. Благодаря работам в области оптимального раскроя основоположника теории линейного программирования лауреата Нобелевской премии академика Л. В. Канторовича задачу оптимального раскроя можно назвать классической прикладной оптимизационной задачей.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь формулировать и использовать для экономического анализа следующие понятия:
• материал;
• заготовка;
• отходы;
• способ раскроя (рациональный и оптимальный);
• интенсивность использования рациональных способов раскроя.
Модели
Большинство материалов, используемых в промышленности, поступает на производство в виде стандартных форм. Непосредственное использование таких материалов, как правило, невозможно. Предварительно их разделяют на заготовки необходимых размеров. Это можно сделать, используя различные способы раскроя материала. Задача оптимального раскроя состоит в том, чтобы выбрать один или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов. Задачи такого типа возникают в металлургии и машиностроении, лесной, лесообрабатывающей, легкой промышленности.
Выделяют два этапа решения задачи оптимального раскроя. На первом этапе определяются рациональные способы раскроя материала, на втором — решается задача линейного программирования для определения интенсивности использования рациональных способов раскроя.
1. Определение рациональных способов раскроя материала.
В задачах оптимального раскроя рассматриваются так называемые рациональные (оптимальные по Парето) способы раскроя. Предположим, что из единицы материала можно изготовить заготовки нескольких видов. Способ раскроя единицы материала называется Рациональным (оптимальным по Парето), если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.
Пусть K — индекс вида заготовки, K = 1,.... Q; I — индекс способа раскроя единицы материала, I = 1,..., Р; аIk — количество (целое число) заготовок вида K, полученных при раскрое единицы материала <-м способом.
Приведенное определение рационального способа раскроя может быть формализовано следующим образом.
Способ раскроя V Называется рациональным (оптимальным по Парето), если для любого другого способа раскроя I из соотношений АIk ³ аVk, k = 1, ..., Q, следуют соотношения АIk = аVk, k = 1, ..., Q.
2. Определение интенсивности использования рациональных способов раскроя.
Обозначения:
J —индекс материала, J = 1,..., П;
K —индекс вида заготовки, K = 1, ..., Q;
I — индекс способа раскроя единицы материала, I = 1,..., Р;
АIjk — количество (целое число) заготовок вида K, полученных при раскрое единицы J-го материала I-м способом;
Bk — число заготовок вида K В комплекте, поставляемом заказчику;
Dj — количество материала J-го вида;
Xji — количество единицу J-го материала, раскраиваемых по I-му способу (интенсивность использования способа раскроя);
Cji — величина отхода, полученного при раскрое единицы J-го материала по I-му способу;
У — число комплектов заготовок различного вида, поставляемых заказчику.
Модель А раскроя с минимальным расходом материалов:
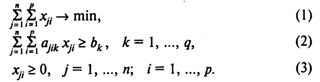
Здесь (1) — целевая функция (минимум количества используемых материалов);
(2) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(3) — условия неотрицательности переменных.
Специфическими для данной области приложения модели линейного программирования являются ограничения (2).
Модель В раскроя с минимальными отходами:

![]()
Здесь (4) — целевая функция (минимум отходов при раскрое материалов);
(5) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(6) — условия неотрицательности переменных.
Модель С раскроя с учетом комплектации:

Здесь (7) — целевая функция (максимум комплектов, включающих заготовки различных видов);
(8) — ограничения по количеству материалов;
(9) — система ограничений, определяющих количество заготовок, необходимое для формирования комплектов;
(10) — условия неотрицательности переменных.
Специфическими для данной области приложения модели линейного программирования являются ограничения (9).
| < Предыдущая | Следующая > |
|---|