02.1. Примеры

Пример 1. Сколько производить?

Предприятие располагает ресурсами сырья и рабочей силы, необходимыми для производства двух видов продукции. Затраты ресурсов на изготовление одной тонны каждого продукта, при­быль, получаемая предприятием от реализации тонны продукта, а также запасы ресурсов указаны в следующей таблице:

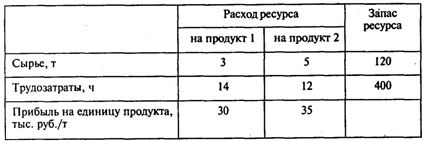
Вопросы:

1. Сколько продукта 1 следует производить для того, чтобы обеспечить максимальную прибыль?

2. Сколько продукта 2 следует производить для того, чтобы обеспечить максимальную прибыль?

3. Какова максимальная прибыль?

4. На сколько возрастет максимальная прибыль, если запасы сырья увеличатся на 1 т?

5. На сколько возрастет максимальная прибыль, если допус­тимый объем трудозатрат увеличится с 400 до 500 ч?

Решение. Пусть Х1 — объем выпуска продукта 1 в тоннах, Х2 — Объем выпуска продукта 2 в тоннах. Тогда задача может быть опи­сана в виде следующей модели линейного программирования:

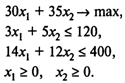
Используя пакет РОМ For WINDOWS (далее - POMWIN), ис­ходную информацию для решения этой задачи можно представить в виде следующей таблицы:

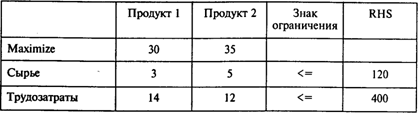
Решая эту задачу, получаем следующий результат:

В нижней строке указан объем выпуска каждого продукта, удовлетворяющий ограничениям на ресурсы и обеспечивающий максимальную прибыль. Величина 988,24 — максимальное значе­ние целевой функции.

Чтобы обеспечить максимальную прибыль, следует произво­дить 16,47 т продукта 1 и 14,12 т продукта 2.

Максимальная прибыль равна 988,24 тыс. руб.

В правом столбце таблицы указаны двойственные оценки для каждого ограничения. Так, величина 3,82 показывает, что при увеличении запаса сырья на 1 т (до 121) максимальное значение целевой функции для нового оптимального плана увеличится по сравнению с 988,24 на 3,82 тыс. руб. Аналогично можно интер­претировать значение двойственной оценки 1,32 для второго ре­сурса.

Следующая таблица содержит дополнительную информацию, предоставляемую пакетом POMWIN:

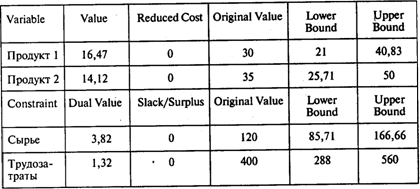
Два правых столбца таблицы — границы устойчивости по зна­чениям коэффициентов целевой функции (верхняя часть табли­цы) и правых частей ограничений (нижняя часть).

Так, в случае если прибыль, получаемая от реализации 1 т про­дукта 1, изменится, но останется в пределах от 21 до 40,83, коли­чество продукта 1 в оптимальном плане не изменится.

В случае если запас сырья изменится, но останется в пределах от 85,71 до 166,66, двойственная оценка этого ресурса не изменится.

Соответственно, если допустимый объем трудозатрат изменит­ся в пределах от 288 до 560 ч, двойственная оценка этого ресурса не изменится.

Если допустимый объем трудозатрат увеличится с 400 до 500 ч, то максимальная прибыль увеличится на 132 тыс. руб.

Пример 2. Производить или покупать?

Фирма производит два типа химикатов. На предстоящий ме­сяц она заключила контракт на поставку следующего количества этих химикатов:

Производство фирмы ограничено ресурсом времени работы двух химических реакторов. Каждый тип химикатов должен быть обработан сначала в реакторе 1, а затем в реакторе 2. Ниже в таб­лице приведен фонд рабочего времени, имеющийся у каждого реактора в следующем месяце, а также время на обработку одной тонны каждого химиката в каждом реакторе:

Из-за ограниченных возможностей, связанных с существу­ющим фондом времени на обработку химикатов в реакторах, фир­ма не имеет достаточных мощностей, чтобы выполнить обязатель­ства по контракту. Выход заключается в следующем: фирма долж­на купить какое-то количество этих химикатов у других производителей, чтобы использовать эти закупки для выполнения контракта. Ниже приводится таблица затрат на производство хи­микатов самой фирмой и на закупку их со стороны:

Цель фирмы состоит в том, чтобы обеспечить выполнение кон­тракта с минимальными издержками. Это позволит ей максими­зировать прибыль, так как цены на химикаты уже оговорены контрактом. Другими словами, фирма должна принять решение: сколько химикатов каждого типа производить у себя, а сколько — закупать со стороны для того, чтобы выполнить контракт с ми­нимальными издержками.

Вопросы:

1. Сколько химикатов типа 1 следует производить фирме?

2. Сколько химикатов типа 2 следует производить фирме?

3. Сколько химикатов типа 1 следует закупать со стороны?

4. Сколько химикатов типа 2 следует закупать со стороны?

5. Каковы минимальные издержки на выполнение контракта?

6. Следует ли изменить объем закупок химикатов типа 2 со стороны, если их цена возрастет до 75 тыс. руб. за тонну?

7. На сколько возрастут минимальные издержки, если фонд времени работы реактора 2 сократится с 400 до 300 ч?

Решение. Введем обозначения:

X1 — количество продукта 1, производимого компанией;

Z1 — количество продукта 1, закупаемого компанией;

X2 — количество продукта 2, производимого компанией;

Z2 — количество продукта 2, закупаемого компанией.

Модель линейного программирования приведена в следующей таблице:

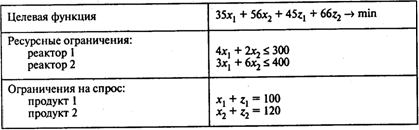
Условия неотрицательности переменных: ; ; ; .

Таблица исходной информации для расчетов в POMWIN имеет следующий вид:

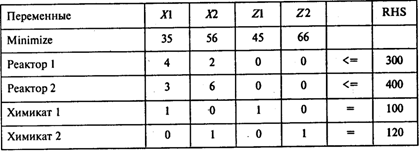
Результаты расчетов:

Таблица двойственных оценок и границ устойчивости:

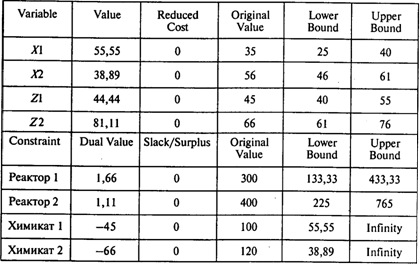
Из таблицы двойственных оценок и границ устойчивости вид­но, что в пределах изменения закупочной цены на химикат типа 2 от 61 до 76 (ее фактическое значение 66) оптимальный план не изменится.

Из таблицы также видно, что изменение ресурса времени ра­боты реактора 2 в пределах от 225 до 765 не приведет к измене­нию двойственной оценки соответствующего ограничения.

Ответы: 1. 55,55 т. 2. 38,89 т. 3. 44,44 т. 4. 81,11 т.

5. 11 475,56 тыс. руб. 6. Нет, не следует.

7. Ha 111 тыс. руб.

< Предыдущая		Следующая >